

|
||
|
|
||
The Lateral Torsional Buckling Check is executed according to EN 1993-1-1 art. 6.3.2.1.
CHS sections (Formcode 3) are taken as non-susceptible to Lateral Torsional Buckling.
RHS sections (Formcode 2) sections are classified as non-susceptible to Lateral Torsional Buckling if the following condition is fulfilled (Ref.[9] pp.119).
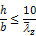
With:
| h |
Height of RHS section |
|
b |
Width of RHS section |
|
|
Relative slenderness for weak axis flexural buckling |
For all other sections the Lateral Torsional Buckling check is executed in which the elastic critical moment for Lateral-Torsional Buckling Mcr is determined by the following formula Ref.[9]:
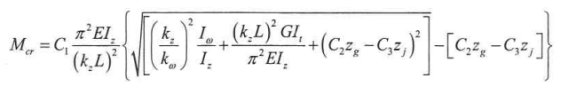
With:
Haunched sections (I+Ivar, Iw+Plvar, Iw+Iwvar, Iw+Ivar, I+Iwvar) and composed rail sections (Iw+rail, Iwn+rail, I+rail, I+2PL+rail, I+PL+rail, I+2L+rail, I+Ud+rail) are considered as equivalent asymmetric I sections.
For advanced Lateral Torsional buckling analysis, see "Annex D: Use of diaphragms ".
The coefficients C1, C2 and C3 can be calculated according to three different methods:
ENV 1993-1-1 Annex F
ECCS 119/Galea
Lopez, Yong, Serna
By default the method according to ECCS 119/Galea is applied.
The following paragraphs give information on these methods.
When this setting is chosen, the moment factors are determined according to ENV 1993-1-1 Annex F Ref.[10].
Detailed information can be found in chapter "Annex C: Calculation of moment factors for LTB".
When this setting is chosen, the moment factors are determined according to ECCS 119 Annex B Ref.[9].
The figures given in this reference for C1 and C2 in case of combined loading originate from Ref.[28] which in fact also gives the tabulated values of those figures as well as an extended range.
The actual moment distribution is compared with several standard moment distributions. These standard moment distributions are moment lines generated by a distributed q load, a nodal F load, or where the moment line is maximum at the start or at the end of the beam.
The standard moment distribution which is closest to the actual moment distribution, is taken for the calculation of the factors C1 and C2.
In case of a linear moment diagram the C1 coefficient is determined using formula (301) of ECCS 119 Annex B Ref.[9].
The coefficient C2 is taken as zero in this case.
In case of Point loading the coefficients C1 and C2 are calculated using tables 5-8 of Galea Ref.[28].
A double interpolation is used for intermediate values.
In case of Line loading the coefficients C1 and C2 are calculated using tables 1-4 of Galea Ref.[28].
A double interpolation is used for intermediate values.
In case k differs from 1.00 the C1 and C2 values determined from Galea Ref.[28] are overruled by the values from ECCS 119 Annex B Ref.[9] tables 63 and 64
For all cases the factor C3 is taken from ECCS 119 Annex B Ref.[9] tables 63 and 64. The C3 value is determined based on the case of which the C1 value most closely matches the table value.
The table for C3 uses the value ψf which is taken as 0 by default.
For asymmetrical I-sections (Form code 101) ψf is calculated as follows:
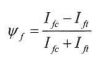
Ifc and Ift concern the moments of inertia of the compression ( c ) and tension ( t ) flange about the minor axis.
For this method ψf should be within the following range:
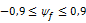
When this is not the case ψf is set to the respective limit and a warning is given.
ECCS 119 Annex B Ref.[9] tables 65 to 68 give values for C1, C2 and C3 for I-section cantilevers.
These coefficients are used only in case the following conditions are met:
A cantilever is defined as a member at the end of a buckling system which has free ends for both buckling about the y-y and z-z axis. In addition, the LTB length should correspond to the full system length of the buckling system.
This method differentiates between ‘warping prevented’ and ‘warping free’ at the fixed end. This setting is taken from the buckling system.
This method uses the value ψf which is calculated as specified above.
For this method ψf should be within the following range:
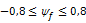
When this is not the case ψf is set to the respective limit and a warning is given.
This method uses the coefficient 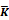 which is defined as follows:
which is defined as follows:
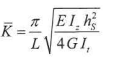
with:
| L |
System length for LTB |
|
E |
Modulus of Young |
|
G |
Shear modulus |
|
Iz |
Inertia about the weak axis |
|
It |
Torsion constant |
|
hs |
Distance defined as follows: Form Code 1: H - t Form Code 101: H – 0,5 * tt – 0,5 * tb |
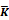 should be within the following range:
should be within the following range:
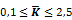
When this is not the case 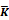 is set to the respective limit and a warning is given.
is set to the respective limit and a warning is given.
In addition this method should be used in combination with k equal to 2,00 and kw equal to 1,00
When this is not the case an additional warning is given.
When this setting is chosen, the moment factors are determined according to Lopez, Yong, Serna Ref.[29].
When using this method the coefficients C2 and C3 are set to zero.
The coefficient C1 is calculated as follows:

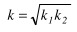
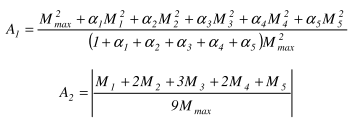
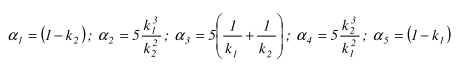
With:
| k1 |
Taken equal to kw |
|
k2 |
Taken equal to kw |
|
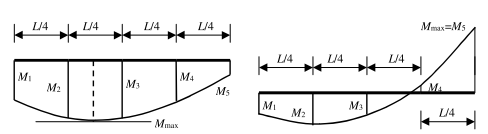
M1, M2, M3, M4, M5 |
The moments My determined on the buckling system in the given sections as shown on the above figure. These moments are determined by dividing the beam into 10 parts (11 sections) and interpolating between these sections. |
|
Mmax |
The maximal moment My along the LTB system. |
This method is only supported in case both k and kw equal 0.50 or 1.00
The distance zg is defined as the distance between the point of load application and the shear center. The point of load application is taken as both the top (+z) and bottom (-z) of the cross-section. Depending on the sign of the moment either the top or the bottom zg is used.
The sign is determined as follows: zg is taken as positive for a Destabilizing load.
For a standard beam, the determination of Stabilizing/Destabilizing is done depending on the moment:
If My > 0 and loading On top => Destabilizing
If My > 0 and loading On bottom => Stabilizing
If My < 0 and loading On top => Stabilizing
If My < 0 and loading On bottom => Detabilizing
For a cantilever, the determination of Stabilizing/Destabilizing will be done depending on the sign of the equivalent lineload:
If q downward and loading On top => Stabilizing
If q downward and loading On bottom => Destabilizing
If q upward and loading On top => Destabilizing
If q upward and loading On bottom => Stabilizing
By setting the point of load application to Always destabilising or Always stabilising the above dependency on the bending moment or loading direction can be overruled.
In case the moment diagram concerns a linear diagram zg = 0.
The distance zj is determined from the βy asymmetry parameter of the cross-section.
If My < 0 => zj = 0,5 * βy
If My > 0 => zj = - 0,5 * βy
In case of an axis switch (Iz > Iy) also βy and βz are switched.
The General case as defined in EN 1993-1-1 art. 6.3.2.2 uses a limit slenderness of 0,2.
For deciding if the LTB check should or should not be executed art. 6.3.2.2(4) refers to the Alternative case which uses a limit slenderness of 0,4.
It is clear that this is an inconsistency within the code. In case for example the slenderness has a value just below 0,4 this would erroneously lead to the conclusion that no LTB check should be done. In this case however the Chi reduction value for curve d for example is 0,85 which indicates a 15% reduction of the bending capacity.
Therefore, conform the theory, for the General case the limit slenderness used in art. 6.3.2.2(4) is set to 0,2.
For the 'Rolled & Equivalent welded case' given in art. 6.3.2.3 the theory in Ref.[9] clearly specifies that it is valid only for I-sections or sections with comparable shape.
Therefore this article is applied only in case of the following form-codes:
- Symmetric I-sections (Formcode 1)
- Asymmetric I-sections (Formcode 101)
A specific National Annex can overrule this condition and use this article also for other sections. For more information reference is made to the Theoretical Background of National Annexes to EN 1993.
In case Lateral-Torsional Buckling curves for the ‘Rolled and equivalent welded’ case are used according to EN 1993-1-1 art. 6.3.2.3 the correction factor kc can be determined in two ways:
- By default, kc is determined from C1 as follows Ref.[30]:
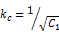
- Alternatively kc can be taken from Table 6.6
The default approach gives a more accurate value for kc compared to the simplified Table 6.6.
The reduction factor for Lateral-Torsional Buckling of Channel sections is determined according to Ref.[22].
More specifically the calculation is done as follows:

This Modified design rule is applied only in case the following conditions are met:
In case the diaphragm is positioned on the compression flange and provides a fully braced support, no LTB check needs to be executed and a note is printed instead.
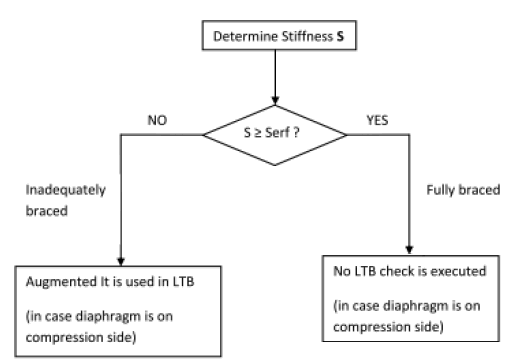
For more information on diaphragms see "Annex D: Use of diaphragms ".
For more information on the calculation of the lateral stiffness see "Use of Diaphragms".