

|
||
|
|
||
The Torsional (-Flexural) Buckling Check is executed according to EN 1993-1-1 art. 6.3.1.4.
In case of an RHS section (Formcode 2) or CHS section (Formcode 3) the check will not be executed and a note will be shown instead.
In case of an I-section (Formcode 1), when the check is not limiting it will not be printed and a note is shown instead. Not limiting is defined here as a unity check lower than the unity check for Flexural Buckling. In case however Flexural buckling can be ignored (due to low compression force or low slenderness) the comparison is done with the unity check of the compression check.
The buckling curve for torsional (-flexural) buckling is taken as the z-z buckling curve according to the table given in "Flexural Buckling".
The value of the elastic critical load Ncr is taken as the smallest of Ncr,T (Torsional buckling) and Ncr,TF (Torsional-Flexural buckling).
The elastic critical load Ncr,T for torsional buckling is calculated according to Ref.[17].
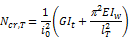
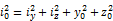
With:
| E |
Modulus of Young |
|
G |
Shear modulus |
|
It |
Torsion constant |
|
Iw |
Warping constant |
|
lT |
Buckling length for the torsional buckling mode |
|
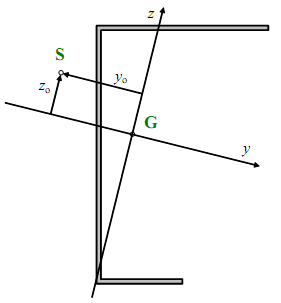
y0 and z0 |
Coordinates of the shear center with respect to the centroid |
|
iy |
radius of gyration about the strong axis |
|
iz |
radius of gyration about the weak axis |
The elastic critical load Ncr,TF for torsional flexural buckling is calculated according to Ref.[17].
Ncr,TF is taken as the smallest root of the following cubic equation in N:
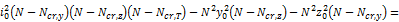 0
0
With:
| Ncr,y |
Critical axial load for flexural buckling about the y-y axis |
|
Ncr,z |
Critical axial load for flexural buckling about the z-z axis |
|
Ncr,T |
Critical axial load for torsional buckling |
In case a diaphragm is used, independent on which side, the augmented It will be used also in Torsional Buckling.
For more information on diaphragms see "Annex D: Use of diaphragms ".