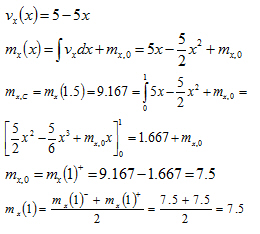|
||
|
|
||
Řešič počítá interně vnitřní síly v integračních bodech a nakonec extrapoluje spočtené výsledky z integračních bodů do uzlů plošného prvku. Při extrapolaci použije vzorce pro hyperbolický paraboloid. Tyto hodnoty se pak prohlásí za neprůměrované uzlové hodnoty. Vyhlazení neprůměrovaných hodnot si ukážeme na příkladu deskového pásu o rozměrech 4x3 m. Deskový pás je prostě podepřen podél kratších stran, Poissonův součinitel μ = 0 a zatížení p = 5 kNm-2. Pás je rozdělen na síť 4x3 konečných prvků a je řešen pomocí Kirchhoffovy a Mindlinovy teorie. Obrázek ukazuje podélný řez uprostřed pásu.
Následující algoritmus se použije na zprůměrování hodnot v uzlech:
Uzlová hodnota se určí jako aritmetický průměr z hodnot v sousedních plošných prvcích. Při zvolení možnosti "průměrované hodnoty na 2D makru" se hodnoty ze sousedních plošných prvků zprůměrují pouze, když prvky leží na jednom 2D makru, na stejné straně případné vnitřní hrany a není-li uzel označen uživatelem jako vnitřní uzel. V takovém případě se hodnoty neprůměrují a v průběhu vnitřních sil se objeví nespojitost.
Např.
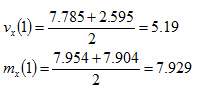
Např.
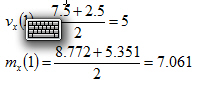
Z předchozího obrázku je vidět, že standardní zprůměrované hodnoty vedou ke skokových změnám hodnot podél okrajů. Příčinou je to, že na okraji není s čím hodnoty průměrovat. Proto se podél okrajů používá jiný postup.
Při zvolení možnosti "průměrované hodnoty na celé konstrukci" se uzly na okraji 2D makra, které není připojeno k jinému 2D makru nebo které je připojeno k makru, jež není vybráno považují za okraj konstrukce. Při zvolení možnosti "průměrované hodnoty na 2D makru" se uzly na všech okrajích 2D makra, uzly na vnitřních hranách a vnitřní uzly definované uživatelem považují za okraj konstrukce. V takových situacích se průměrování provede ve dvou krocích. V prvním kroku se spočtou zprůměrované uzlové hodnoty v uzlech, které neleží na okraji konstrukce. Hodnoty v uzlech prvků, které leží podél okraje konstrukce se vypočtou takovým algoritmem, který uchová původní hodnoty ve středech prvků. Ve druhém kroku se spočtou zprůměrované uzlové hodnoty v uzlech, které leží na okraji konstrukce.
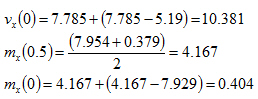
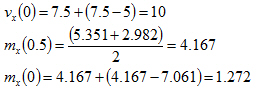
Kirchhoffova teorie počítá smykové síly jako třetí derivaci průhybu:
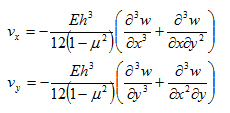
Při výpočtu třetí derivace se projeví značná ztráta přesnosti. Proto se hodnoty smykových sil spočtených řešičem podle Kirchhoffovy teorie nepoužijí ale vpočtou se vylepšeným algoritmem využívajícím derivace momentů:
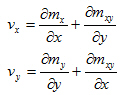
Rovnice využívají hodnoty momentů mx, my a mxy zprůměrované podle kroků (a) a (b), což vede k přesnějším hodnotám smykových sil než jaké jsou spočteny řešičem.
U Mindlinovy teorie se smykové síly počítají jako první derivace průhybu.
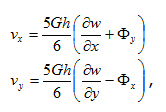
tyto hodnoty se určí řešičem a jsou přímo použity.
Smykové síly se potom průměrují podle zvoleného postupu pomocí kroků (a) a (b).
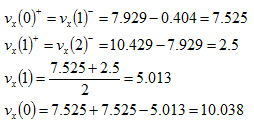
Zatímco hodnoty momentů v integračních bodech odpovídají teorii, jejich extrapolace do uzlů s použitím hyperbolického paraboloidu vedou k jisté ztrátě přesnosti. Důvodem je to, že hyperbolický paraboloid nenahrazuje průběh momentů po prvku s dostatečnou přesností. Výpočet hodnot momentů v uzlech využívá vylepšený algoritmus, který nahrazuje extrapolaci hyperbolickým paraboloidem vylepšenou metou integrace smykové síly. Protože se předpokládá , že průběh smykových sil po povrchu prvku sleduje tvar hyperbolického paraboloidu (plocha druhého řádu), integrál tohoto povrchu představuje plochu třetího řádu, který aproximuje průběh momentů s vyšší přesností. Toto je založeno na výše uvedených rovnicích pro výpočet smykové síly s použitím derivace momentů. Momenty se pak zapíší jako:
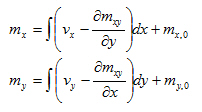
Integrační konstanty mx0, my0 se vypočtou z podmínek pro hodnotu uprostřed prvku.
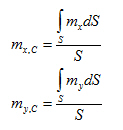
kde S je plocha prvku. Hodnoty vnitřních sil se vypočtou pomocí kroků (a), (b) a (c), integrály se vyčíslí numerickou integrací. Získané hodnoty momentů v uzlech se pak použijí podle zvolené průměrovací volby zprůměrují podle kroku (a).
Např.
První prvek
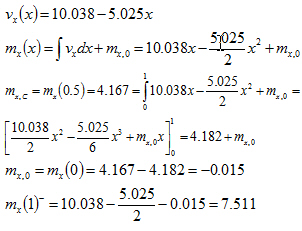
Druhý prvek
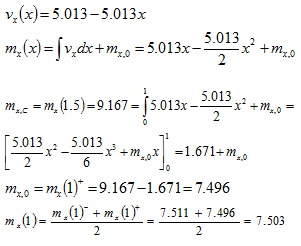
Např.
První prvek
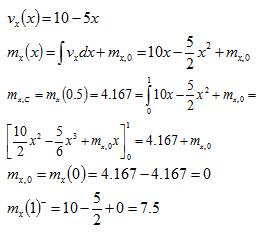
Druhý prvek