|
||
|
|
||
Termíny výpočet (nebo analýza) FNL (fyzikálně nelineární výpočet) a výpočet (nebo analýza) FGNL (fyzikálně a geometricky nelineární výpočet) jsou přejaty z předchozích verzí softwaru. Tyto termíny jsou velmi podobné a mohou být mírně matoucí.
Proto je užitečné začít stručným popisem rysů a principů těchto dvou druhů analýzy.
Nejprve by bylo rozumné uvést lépe vysvětlující jména.
To, co bylo známo jako výpočet FNL, by se mělo nazývat:
Výpočet průhybů podle normy.
DŮLEŽITÉ: Počínaje verzí 2008.1 byl termín FNL nahrazen vhodnějším označením Normově závislé průhyby (NZP).
To, co bylo známo jako FGNL výpočet by se mělo nazývat:
fyzikálně (a geometricky) nelineární výpočet.
Není pravidlem, že se v rámci tohoto výpočtu musí použít oba typy nelinearit. Jsou zde tři možnosti:
(i) bere se v úvahu pouze fyzikální nelinearita,
(ii) bere se v úvahu pouze geometrická nelinearita,
(iii) berou se v úvahu obě tyto nelinearity (fyzikální i geometrická).
Tento fakt může střídavě vést ke zkracování označení druhého typu výpočtu na „fyzikálně nelineární výpočet“ (FNL). Nyní jsou zřejmé důvody, proč bylo nutno zavést rozumnější pojmenování.
Druhý důvod je, že staré výpočty FNL (od verze 2008.1 NZP) nejsou ve skutečnosti fyzikálně nelineární výpočty ve smyslu metody konečných prvků (narozdíl od FGNL, což je skutečný nelineární výpočet). Je to řešení o dvou krocích přesně následující dané předpisy v technických standardech pro návrh a kontrolu betonových konstrukcí.
Obě analýzy jsou v první řadě zaměřeny na betonové konstrukce. Výpočet průhybů podle normy“ je určen výhradně pro betonové nosníky a desky, neboť je založen na technických standardech pro návrh a kontrolu betonových konstrukcí.
Fyzikálně (a geometricky) nelineární výpočet“ je obecná procedura přizpůsobená analýze betonových rámů (bere v úvahu určené vyztužení), neomezuje se však pouze na tyto struktury.
Tento výpočet průhybů je založen na příslušné technické normě. Proto také představuje výpočet svázaný s normou, který se provádí ve dvou krocích. Nejprve se provede normální lineární výpočet a vypočtené vnitřní síly jsou použity k vložení výztuže (zadaná výztuž) nebo přinejmenším k určení požadované plochy výztuže. Tato procedura pokračuje výpočtem trhlin a jejich vlivem na tuhost jednotlivých prvků. Toto oslabení je následně vloženo do řešiče. Nakonec se výpočet (lineární) spustí ještě jednou s tím, že se bere v úvahu takto redukovaná tuhost. Což je právě to, co technické normy požadují.
Je vypočítán krátkodobý průhyb. Tento průhyb je vynásoben součinitelem dotvarování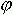 
, čímž se získá dlouhodobý průhyb. Je známo, že elastický průhyb, vynásobený součinitelem dotvarování 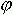udává průhyb způsobený dotvarováním. Poté sečteme dlouhodobý a krátkodobý průhyb a získáme absolutní průhyb, který může být vyhodnocen v souladu s normou.
Tento výpočet vlivu dotvarování je zjednodušený a může být použit pouze pro určité situace. Ve skutečnosti to v případě vyztuženého betonu pokrývá většinu možných situací, neboť nemusí být sledována historie postupu výstavby. Jinými slovy, pokud nemusí být sledována historie postupu výstavby, je možné tento postup použít.
Postup je založen na metodě efektivního modulu elasticity Ef:
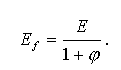
Fyzikálně (a geometricky) nelineární výpočet (dosud nazývaný FGNL) je zcela odlišný. Jde o fyzikálně anebo geometricky nelineární výpočet, který může být použit na rámové konstrukce, narozdíl od Výpočtu průhybu podle normy, který se může použít i pro analýzu desek. Fyzikálně (a geometricky) nelineární výpočet může být použit pro rovinnou nebo prostorovou rámovou konstrukci. Pokud je součástí analyzované struktury deska (nebo obecně skořepina), je takovýto model také analyzován, ale deska (skořepina) je brána jako lineární element. Stejný přístup je používán, pokud se v modelu konstrukce objeví ocelový nosník (nebo nosník z jiného materiálu).
Pro rámové konstrukce bereme v potaz efekt trhlin, plasticitu a další faktory působící na tuhost. Problém je řešen prostředky skutečného nelineárního výpočtu s použitím iterace a sečných metod, to jest Newton-Raphsonovou metodou, jak je implementována v systému SCIA Engineer. Je proveden úplný fyzikálně anebo geometricky nelineární výpočet. V části Funkcionalita je třeba určit, jaká nelinearita má být použita: (i) fyzikální, (ii) geometrická, nebo (iii) obě. Díky tomuto nastavení řešič rozpozná, jaký typ výpočtu má provést.
Přidáme určité zatížení, abychom mohli zjistit, k jakému praskání dojde a tím určit oslabení v řezu (ve skutečnosti je to trochu složitější, ale plný popis problému překračuje rámec tohoto textu, podrobnosti viz [1]). V místech, kde se objeví trhliny, je tuhost upravena a výpočet se spustí znovu. Vypočteme vnitřní síly, které jsou založeny na upravené tuhosti, tyto nové vnitřní síly však obvykle stále nekorespondují s tuhostí. Proto musíme určit tuhost ještě jednou. Tato procedura pak pokračuje tolikrát, kolikrát je potřeba k dosažení konvergenčního kritéria. Fyzikálně (a geometricky) nelineární výpočet je prováděn v několika (obvykle mnoha) krocích a výsledek je takový stav konstrukce, kdy je napětí v rovnováze s vnitřními silami (narozdíl od Výpočtu průhybu podle normy).
To je způsob, jak najít mezní únosnost nejenom jednoho řezu, ale celé konstrukce. A to je také hlavní cíl Fyzikálně (a geometricky) nelineárního výpočtu.