

|
||
|
|
||
|
Jméno |
Je použito pro označení (identifikaci) zatížení |
|
Epsilon [mm/m’] |
Relativní prodloužení v důsledku zvýšení teploty nebo smrštění. |
|
k [mrad/m’] |
Zakřivení roviny v důsledku nerovnoměrného oteplení nebo smrštění. |
Pokud uvažujeme, že materiál je homogenní a izotropní a teplota je po tloušťce průřezu rozložena lineárně, lze prodloužení plochy v důsledku oteplení spočítat jednoduše.
Předpokládejme nárůst teploty na horní ploše TH a nárůst teploty na dolní ploše TD. Výsledný nárůst teploty (smrštění) pak lze rozložit do dvou složek - viz obrázek dole.
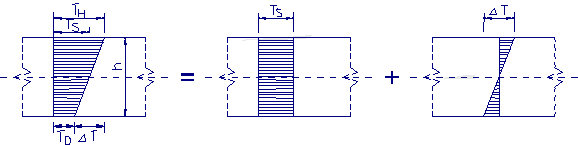
Pak dostaneme:
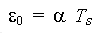
kde
|
Alpha |
Součinitel tepelné roztažnosti |
|
Ts |
Zvýšení teploty |
Kladný nárůst teploty vyvodí kladné hodnoty prodloužení.
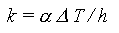
kde
|
Alpha |
Součinitel tepelné roztažnosti |
|
delta T |
Rozdíl teplot mezi povrchy z = -h/2 a z = +h/2. |
|
H |
Tloušťka prvku |
Z geometrie vyplývá, že k = 1 / R, kde R je poloměr kulové plochy, jejíž tvar plocha zaujme, pokud není zabráněno změně tvaru v důsledku změny teploty.
Poznámka: Pokud není nárůst teploty po délce průřezu lineární, je nutné průběh teploty linearizovat. Výsledky je pak potřeba upravit a přičíst k nim napětí od rozdílu daného a linearizovaného oteplení, získané zvláštním výpočtem.
Příklad
Následující předpokládaná – dosti teoretická – situace. Mějme kruhovou plochu podepřenou v jejím středu.
Za prvé, nechme tuto plochu rovnoměrně prodloužit o 10 mm/m. Předpokládejme, že oba povrchy plochy jsou zahřívány.
Po výpočtu je vidět výsledné a symetrické roztažení plochy (obrázek ukazuje obě počáteční plochy a deformovanou síť konečných prvků).
Za druhé, nechme plochu nerovnoměrně prodloužit (zakřivit) o 10 mrad/m. Předpokládejme, že je zahříván pouze jeden povrch plochy.
Po výpočtu je vidět, že se plocha při tomto typu zatížení deformuje na miskovitý tvar. Obrázek ukazuje obě počáteční plochy a deformovanou síť konečných prvků. Na druhém obrázku je názornější pohled ze strany.