

|
||
|
|
||
Otevřete servis Konstrukce.
Použijte jakoukoli funkci pro zadání plošného prvku (rovinný plošný prvek, stěna, skořepina).
Zobrazí se dialogové okno vlastností.
Vyplňte potřebné parametry.
Nastavte parametr Model MKP na Ortotropní.
V dialogovém okně se objeví nová položka: Ortotropie.
Klikněte na tlačítko se třemi tečkami [...] v tomto přidaném řádku.
Zobrazí se okno s parametry ortotropie.
Zadejte správné hodnoty.
Potvrďte tlačítkem OK.
Potvrďte dialogové okno vlastností desky.
Zadejte plošný prvek.
DŮLEŽITÉ: Směr ortotropie je obecně definován osou x konečného prvku. Jestliže je ortotropní plošný prvek zadán pomocí funkce Deska, je možné řídit směr ortotropie. Lokální osa x každého konečného prvku následuje směr lokální osy x desky. Jestliže se lokální osa x desky pootočí, směr ortotropie se pootočí také. Jestliže je ale deska zadána pomocí funkce Skořepina, nelze explicitně řídit směr lokální osy x jednotlivých konečných prvků. Jestliže se tudíž ortotropie má aplikovat na váš model, MUSÍ být jako Deska a ne jako Skořepina.
Existují dva případy ortotropie:
fyzikální ortotropie způsobená odlišnými moduly ve směrech x a y, tj. skutečná materiálová charakteristika závisející na technologii výroby materiálů (různé vrstvy, dřevo, atd.)
technická nebo tvarová ortotropie žebrovaných desek / stěn
Nejprve popíšeme parametry fyzikální ortotropie. Ortotropní materiál je definován následujícími fyzikálními konstantami:
h E1 E2 G1212 G13 G23
Hodnota 21 se určuje takto:
v21 = v12 * E2/E1
Smykový modul G12 se určuje pomocí Kirchoffovy desky:
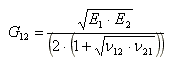
Parametry G13 a G23 jsou nezbytné, protože se používá prvek Mindlinovy desky, u něhož je podstatný vliv smykových sil qx a qy na deformace.
Předpokládáme desku/stěnu s rovnoměrnou tloušťkou h.
Parametry vložené do programu se vypočítají z těchto fyzikálních konstant následujícím způsobem:
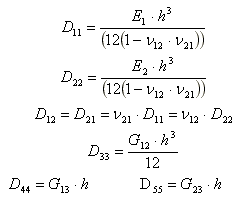
Pro deskový prvek lze vložit úhel Beta mezi směrem 1 (pro který se parametry ortotropie zadávají) a lokální osou x daného prvku.
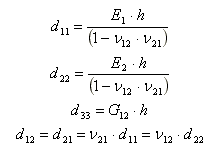
Skořepinový prvek je deskový/stěnový prvek a má oba typy fyzikálních konstant, aniž by měl nějaké další konstanty.
Pro technickou nebo tvarovou ortotropii odkazujeme na publikaci Teorie desek a skořepin P. Timoshenka a S. Woinowského (Theory of plates and shells, McGraw Hill, druhé vydání, 1987). Vztah mezi ohybovými momenty a zakřivením ortotropní desky je dán následujícím vztahem:
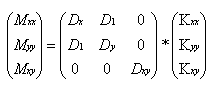
Zadání momentů a zakřivení je následující:
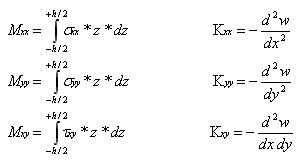
V programu se používají tyto symboly:
D11 = Dx
D22 = Dy
D33 = 0.5 Dxy
D12 = Dx
D44 a D55 jsou přidány, protože se používají Mindlinovy prvky s deformací od smykové síly. V mnoha případech pro výpočet těchto tuhostí neexistují žádné jednoduché vzorce. Deformace od smykové síly je zanedbána (stejně jako u dalších prvků MKP), když jsou pro tyto dvě konstanty zadány velké hodnoty. Doporučení pro výpočet těchto součinitelů v některých praktických případech následuje níže.
Výrazy (vzorce) uvedené pro tuhosti se lehce upravují v závislosti na použitém materiálu. Obzvláště všechny hodnoty pro tuhost v kroucení Dxy založené na čistě teoretických úvahách, by měly být chápány jako první aproximace a pro získání spolehlivějších hodnot modulu G je třeba provést přímé testování. Obvyklé hodnoty pro tuhost v některých praktických případech jsou uvedeny níže:
Izotropní deska s konstantní tloušťkou je definována: tloušťkou h, modulem pružnosti E a Poissonovým součinitelem:
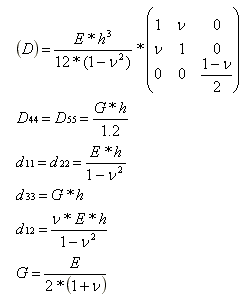
Es je Youngův modul pro ocel, Ec pro beton, c Poissonův poměr pro beton, a platí, že n = Es / Ec. Pro desku s dvousměrnou výztuží ve směrech x a y můžeme předpokládat:
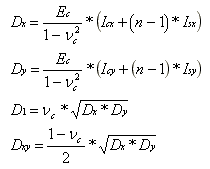
V těchto rovnicích je Icx moment setrvačnosti deskového materiálu, Isx moment setrvačnosti výztuže kolem neutrální osy v řezu x = konstantní, a Icy a Isy jsou příslušné hodnoty pro řez y = konstantní.
Je zjevné, že tyto hodnoty nejsou nezávislé na stavu betonu. Například jakákoli odlišnost ve výztuži ve směrech x a y ovlivní poměr Dx / Dy mnohem více po vzniku trhlin v betonu než před tím.
V tomto případě může teorie ortotropní desky poskytnout jen hrubou představu o skutečném napětí a přetvoření desky.
Platí, že:
E = modul pružnosti materiálu (např. betonu)
I = moment setrvačnosti průřezu T o šířce a1
Az = smyková plocha průřezu T o šířce a1
C = tuhost v kroucení pro jedno žebro
= h / H
Když zadáte tento průřez T, pak jsou geometrický řez, I, Az a C automaticky vypočteny programem.
Poté můžeme předpokládat:
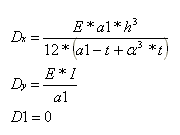
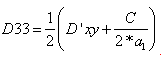
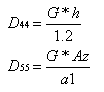
kde D’xy je tuhost v kroucení desky bez žebra
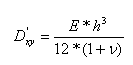
To lze ověřit tak, že se žebro nevezme v úvahu. Řešení musí být stejné jako u izotropní desky v sekci b.1.
Rošt se skládá ze dvou systémů rovnoběžných nosníků rozmístěných v rovnoměrných vzdálenostech podél směrů x a y a pevně spojených v bodech protínání. Nosníky jsou podepřeny na koncích a zatížení je aplikováno kolmo na rovinu xy. Jestliže vzdálenosti a1 a b1 mezi nosníky jsou malé ve srovnání s rozměry roštu a a b, a jestliže ohybová tuhost všech nosníků rovnoběžných s osou x se rovná I1 a ohybová tuhost všech nosníků rovnoběžných s osou y se rovná I2, součinitele jsou následující:
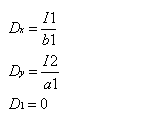
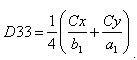
Pro všechny typy prvků se musí tloušťka, která je brána v úvahu pro výpočet mrtvé váhy, zadat do pole Zat. t. Tato tloušťka se násobí hustotou vybraného materiálu.
Další informace najdete v samostatném dokumentu Library_of_Orthotropy_Theory_enu.pdf, obsaženém na instalačním disku DVD.