Open topic with navigation

Výpočet Soilinu

Iterační cyklus soilinu

Hodnoty pro horní stavbu a základy jsou počítané FEM. Tyto hodnoty jsou poté použity jako vstupní data pro soilin.

Iterace je zastavena, když se kontaktní napětí σ_z a posun u_z významně neliší ve dvou po sobě následujících cyklech. Pro toto porovnání je použitá kvadratická norma, která je spočítána po každém cyklu.

Diagram iteračního cyklu:

1. Hodnoty jsou brány z nastavení řešiče, jsou předem definované uživatelem.
2. Data horní konstrukce a základů.
3. FEM výpočet – Důležité výsledky jsou kontaktní napětí σ_z a posun u_z.
4. Výsledky i-té iterace.
5. Porovnání kontaktních napětí σ_z s u_z – je založeno na kvadratické normě, ve chvíli, kdy se již výrazně nezmění, je kalkulace hotová a SCIA Engineer zobrazí výsledky.
6. 1. krok soilinu – kontaktní napětí je přepočítáno na nové zatížení.
7. 2. krok soilinu – C parametry jsou přepočítány, nové zatížení se bere z předchozího kroku
8. 3. krok – výsledné C parametry ze soilinu jsou nové vstupní parametry.
9. Nové C parametry jsou použité v dalším výpočtu FEM.

Po dokončení iterací je zobrazena hláška.

Kvadratická norma pro porovnání výsledků z poslední a předposlední iterace

Výpočet sedání podloží a následné stanovení C parametrů je provedeno standardním způsobem – použití iteračního cyklu. Výsledky tohoto procesu je stav, kdy se kontaktní napětí nebo posun u_z ve dvou po sobě jdoucích cyklech příliš neliší. Z tohoto důvodu je následující kvadratická norma vyčíslena po každé j-té iteraci:

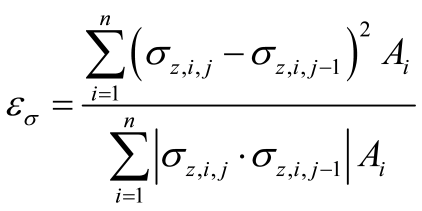
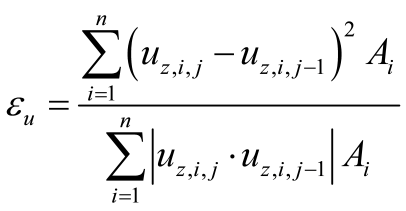
Kde:

npočet uzlů

σ_z,ikontaktní napětí v uzlu i

A_iplocha odpovídající uzlu i

u_z,iglobální posun uzlu i ve směru z

Kalkulace je zastavena když ε_σ<0,001 nebo ε_u<0,001.

Teorie o derivačním procesu

V tomto textu se omezujeme jen na stručnou derivaci za účelem následujícího vysvětlení:

Vzorec pro potenciální energii vnitřních sil 3D modelu má tuto podobu:

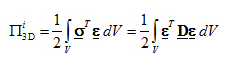
Při zanedbání vlivu vodorovných složek deformace dostaneme následující vektory:

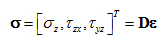
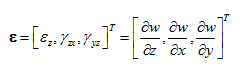
Z toho vyplývá odpovídající zjednodušení matice fyzikálních konstant D.

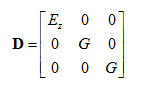
Abychom mohli problém převést z prostoru do roviny, musíme integrovat vzorec 1) podle osy z. Proto se zavádí určitá „tlumicí funkce” f_z která je definována poměrem sednutí v dané hloubce k sednutí povrchu w₀(x,y).

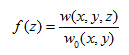
Upravením vektorů 2) dostaneme:

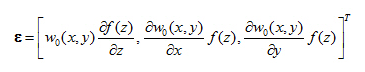
Vložením vektoru 5) do vzorce pro výpočet potenciální energie tělesa V=ΩH, kde Ω je rozsah rovinného modelu a H je hloubka deformované zóny prostorového modelu, dostaneme následující vzorec



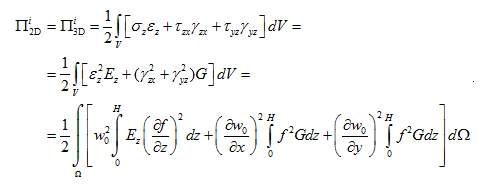
Integrováním přes z, dostaneme vzorec pro výpočet potenciální energie vnitřních sil rovinného modelu se dvěma parametry C₁^S a C₂^S:

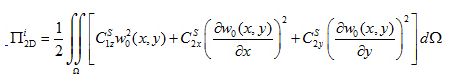
Na základě porovnání vektorů 6) a 7), můžeme definovat vztah mezi parametry obecného modelu (3D) a modelu povrchu (2D):

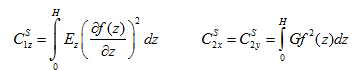
Závěr:

Je tedy možné vyloučit automatický výpočet některých parametrů C a zadat je ručně. To lze dosáhnout speciální úpravou parametrů podloží a nastavením typu Oba (!).

Open topic with navigation