|
||
|
|
||
EN 1992-1-1 definuje několik metod pro analýzu účinků druhého řádu pro osové zatížení (obecnou metodu, zjednodušenou metodu založenou na nominální tuhosti, zjednodušenou metodu založenou na jmenovité křivosti ... ). SCIA Engineer umožňuje provést analýzu účinků druhého řádu pomocí následujících metod:
Obecná metoda ve SCIA Engineer je založena na fyzikálně nelineárním výpočtu (modul FNL), který lze použít pouze pro 1D dílce. Geometrické nelinearity a počáteční deformace lze také zohlednit.
Kroky pro výpočet:
Účinky druhého řádu lze ignorovat, pokud jsou menší než 10 % odpovídajících účinků prvního řádu. Tuto podmínku lze ve SCIA Engineer analyzovat výpočtem stability, viz kapitola Nastavení dat o vzpěru nebo Data prutu o vzpěru. To znamená, že pokud jsou kritické součinitele zatížení u všech stabilitních kombinací větší než 10, pak konstrukce není citlivá na účinky druhého řádu.
Zaškrtávací políčko fyzikální nelinearita pro železobeton v dialogu data projektu na kartě funkcionalita musí být pro použití modulu FNL zaškrtnuto (Obecná metoda). Pokud chceme zohlednit také geometrickou nelinearitu, je třeba zaškrtnout rovněž políčko Počáteční deformace a křivost a 2. řád - geometrická nelinearita.
Pro fyzikálně nelineární výpočet (modul FNL) je třeba definovat speciální data dílce: Nosník - FNL data dílce (strom Konstrukce > Výpočtová data).
Tyto údaje musí být definovány pro každý 1D dílec a uživatel může definovat prostřednictvím těchto údajů následující vlastnosti:
- Bez výztuže - výztuž nebude brána do úvahy.
- Pouze skutečná - uvažuje se uživatelem zadaná skutečná výztuž (volné pruty nebo výztuž zadaná prostřednictvím Redes) na dílci
- Pouze návrhová As - nutná výztuž navržená ve stromu Návrh dílce - návrh (strom Pokročilý beton > 1D dílce) . To znamená, že nutná výztuž musí být na dílci navržena před nelineárním výpočtem.
- 1. skutečná, 2. návrhová - pokud je na dílci zadána uživatelská výztuž, pak je zohledněna. Jinak je použita nutná výztuž - pokud je spočtena.
- 1. návrhová, 2. skutečná - pokud je na dílci spočtena nutná výztuž, pak je zohledněna. Jinak je použita uživatelem zadaná výztuž.
Pokud nejsou FNL data definována na všech 1D dílcích, program vydá upozornění (viz obrázek) před spuštěním nelineárního výpočtu.
Nelineární kombinace musí být zadána před fyzikálně nelineárním výpočtem (obecná metoda). Nelineární kombinaci lze vytvořit ručně nebo automaticky z lineární kombinace.
- pro zadání nelineární kombinace je nutno zohlednit součinitel zatížení
- nelineární kombinace může být vytvořena z lineární normově závislé kombinace pomocí součinitele zatížení podle následujícího postupu:
Klepněte na tlačítko Nové z lineárních kombinací v dialogu Nelineární kombinace
Změňte reprezentaci kombinace na Obsah kombinace v dialogu Kombinace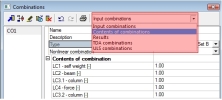
Vyberte jeden obsah kombinace a zavřete dialog
Uživatel může definovat počáteční deformace a zakřivení pro každou nelineární kombinaci. Podle EN 1992-1-1 čl. 5.2, je nezbytné definovat geometrické imperfekce také pro nelineární kombinace. Je mnoho možností pro definici geometrických imperfekcí pro nelineární kombinaci. Podrobný popis definování geometrické imperfekce naleznete v [5].
Imperfekce definovaná prostým nakloněním Imperfekce definovaná funkcí naklonění
Hodnota prostého naklonění v obou směrech se spočte podle EN 1992-1-1 článku 5.2 (5-7) nebo s pomocí prezentovaných hodnot vnitřních sil ve stromu betonu (viz kapitola Výpočet přepočtených ohybových momentů pro sloupy)
Je nezbytné zadat několik nelineárních kombinací s různým směrem (znaménkem) naklonění, protože imperfekce může působit k kladném i záporném směru (v závislosti na zvoleném globálním směru).
Pracovní diagram betonu a výztuže pro nelineární výpočet lze zadat v dialogu Definice materiálu ve skupině EN 1992-1-1 > nelineární chování.
Pracovní diagram materiálů pro FNL výpočet by měl být upraven podle EN 1992-1-1, čl. 5.8.6 (3).
Pracovní diagram pro beton podle 3.1.5 (výraz 3.14 ) v EN 1992-1-1 lze použít pro FNL analýzu. S pracovními diagramy založenými na návrhových hodnotách se návrhová hodnota mezního zatížení získá přímo z výpočtu. Ve výrazu (3.14), a v k - hodnotě:
Dotvarování může být zohledněno podle EN 1992-1-1, čl. 5.8.6 (4). To znamená, že hodnoty přetvoření v pracovním diagramu betonu lze vynásobit součinitelem 1+fef, kde fef je efektivní poměr dotvarování podle 5.8.4. Idealizovaný diagram a návrhový pracovní diagram pro beton C30 / 37 s dotvarováním a bez něj jsou na následujícím obrázku
Předdefinovaný diagram for nelineární výpočet v SCIA Engineer se vypočte pro hodnoty fcm a Ecm bez vlivu dotvarování. Pro definici návrhového pracovního diagramu pro FNL výpočet je nutno opravit hodnoty v předdefinovaném diagramu nebo je nutno definovat nový uživatelský diagram (výběrová položka Napětí/Přetvoření = Uživatelská definice) v dialogu Uživatelská definice
Hodnota poměru dotvarování pro výpočet efektivního poměru dotvarování se vypočítá podle EN 1992-1-1 přílohy B.1 nebo může být hodnota načtena z dat dílce pro beton.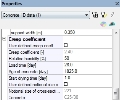
Použít lze návrhový pracovní diagram výztužné oceli uvedený v 3.2.3 (obrázek 3.8) v EN 1992-1-1. S pracovními diagramy založenými na návrhových hodnotách se návrhová hodnota mezního zatížení získá přímo z výpočtu. Předdefinovaný diagram for nelineární výpočet ve SCIA Engineer se vypočte pro hodnoty fyk,tzn. použije se idealizovaný diagram. Pro definici návrhového pracovního diagramu pro FNL výpočet je nutno opravit hodnoty v předdefinovaném diagramu nebo je nutno definovat nový uživatelský diagram (výběrová položka Napětí/Přetvoření = Uživatelská definice) v dialogu Uživatelská definice
Důležitým parametrem pro obecnou metodou je správná hodnota efektivní délka sloupu. Je mnoho možností pro nastavení nebo výpočet efektivní délky sloupu, viz kapitola Data prutu o vzpěru. Účinek druhého řádu se ověří v deformovaném stavu konstrukce podle EN 1992-1-1, čl. 5.8.2 (2). Z toho vyplývá, že efektivní délka sloupu by se měla spočítat rovněž po nelineárním výpočtu. Tyto efektivní délky lze v programu počítat s využitím lineárního stabilitního výpočtu po geometrickém nelineárním výpočtu (sekvenční analýza). Nelineární proces se provede následujícím způsobem;
Následující postup je nutný pro nastavení lineárního stabilitního výpočtu po geometrickém nelineárním výpočtu (sekvenční analýza):
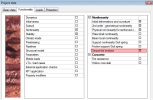
Srovnání výpočtu součinitele vzpěru pro různé metody je uvedeno v přiložené tabulce. Toto srovnání bylo provedeno pro sloup jednoduchého rámu, viz kapitola Zjednodušená metoda.
Před spuštěním nelineárního výpočtu je nezbytné zkontrolovat a nastavit některé jeho parametry.
Existují dvě základní skupiny pro nastavení nelinearity:
• Skupina Nelinearita pro nastavení parametrů geometrické nelinearity, kde nejdůležitějším parametrem je typ metody, která se použije pro výpočet účinků druhého řádu (výběrová položka Geometrická nelinearita - II. řád). K dispozici jsou tři typy metod:
Podrobnější informace o těchto metodách naleznete v [5]
skupina Fyzikální nelinearita pro nastavení parametrů fyzikální nelinearity, kde se nastavují kritéria konvergence a počet kroků pro výpočet nelineárních tuhostí podle vstupních parametrů
Parametr, který má vliv na výpočet nelineární tuhosti, je Součinitel pro výztuž. Nutná nebo uživatelem zadaná výztuž pro všechny dílce, která se použije pro výpočet nelineární tuhosti, se vynásobí tímto součinitelem. Umožňuje rychle zvýšit nebo snížit množství výztuže pro výpočet nelineární tuhosti, pokud by nebylo dosaženo kritéria konvergence. K dispozici je tabulka nelineárních tuhostí dílce s uživatelem zadanou výztuží pro různé hodnoty součinitele vyztužení
Po provedení FNL výpočtu by se konstrukce měla zkontrolovat v servisu FNL napětí/přetvoření a FNL tuhost (strom Výsledky > Pruty), protože pouze v těchto funkcích je nelineární tuhost zohledněna (pracovní diagram pro nelineární výpočet).
Ohybový moment ukázaný v servisech FNL napětí/přetvoření, FNL tuhost a ve všech servisech ve stromu Pokročilý beton se přepočítává k těžišti průřezu s nelineární tuhostí. Pouze v servisu Vnitřní síly na prutech (strom Výsledky > Pruty) jsou ohybové momenty přepočítány k těžišti betonového průřezu. Hodnota ohybového momentu v servisu Vnitřní síly na prutech lze vypočítat z ohybového momentu uvedeného v servisu FNL a ve všech betonových servisech podle vzorce:
kde
My(z),INT ohybový moment kolem osy y(z) uvedený v servisu přepočtených vnitřních sil na prutu
N normálová síla
My(z),PNL ohybový moment kolem osy y(z) uvedený ve FNL servisech a ve všech betonových servisech
ez(y) vzdálenost (excentricita) těžiště betonového průřezu od těžiště průřezu s nelineární tuhostí uvedeným v numerických výstupech v servisu FNL napětí/přetvoření, FNL tuhost, viz kapitola FNL napětí/přetvoření.
Srovnání ohybových momentů My podél dílce v servisu Vnitřní síly na prutu (strom Výsledky) a v servisu Vnitřní síly (strom Pokročilý beton) a přepočet ohybového momentu jsou uvedeny v tabulce
Hlava sloupu:
My,PNL= -104,34 kNm; ez = -7,61mm; N= -1135,33 kN;
My,INT = My,PNL + N•ez = -104,34+(-1135,33•(-0,0076))=-95,70 kNm
Pata sloupu:
My,PNL= 70,85 kNm; ez = -2,81mm; N= -1151,23 kN;
My,INT = My,PNL + N•ez = 70,85+(-1151,23•(-0,0028))=-74,10 kNm
Pro všechny posudky ve stromu Pokročilý beton se pro posudky a návrh použije pracovní diagram zadaný ve skupině Pracovní diagram. To znamená, že v těchto servisech se nezohledňuje pracovní diagram pro nelineární výpočet.
Pokud jsou vnitřní síly vypočteny s použitím nelineárního výpočtu a jsou použity servisy ve stromu Pokročilý beton, pak zaškrtávací políčko Použít data vzpěru v řešiči pro beton (kapitola Data o vzpěru) nebo v datech betonového dílce (kapitola Skupina Výpočet sloupu) musí být vypnuto, protože by se účinky druhého řádu jinak počítaly dvakrát (obecnou metodu a také zjednodušenou metodou)
Tato služba umožňuje vyhodnotit napětí a přetvoření v betonu a ve výztuži a to jak numericky, tak graficky.
Podrobné hodnoty lze posoudit prostřednictvím tlačítka akce Posudek prutu
Ohybové momenty zobrazované v této funkci jsou přepočtené do těžiště průřezu s nelineární tuhostí. Vzdálenost (excentricita) těžiště betonového průřezu a těžiště průřezu s nelineární tuhostí je uvedena v číselném výstupu (hodnoty ey a ez)
Hodnoty N, My, Mz, ey a ez mohou být do tabulky přidány vybráním v dialogu Editoru tabulky (přes ikonu Editor tabulek v Náhledu.)
Tato funkce umožňuje vyhodnotit nelineární tuhost číselně i graficky. Nelineární tuhost je vypočítána v těžišti konečného prvku a hodnota je po celé délce konečného prvku konstantní
Ohybové momenty zobrazované v této funkci jsou přepočtené do těžiště průřezu s nelineární tuhostí. Vzdálenost (excentricita) těžiště betonového průřezu a těžiště průřezu s nelineární tuhostí je uvedena v číselném výstupu (hodnoty ey a ez)
Hodnoty N, My, Mz, ey a ez mohou být do tabulky přidány vybráním v dialogu Editoru tabulky (přes ikonu Editor tabulek v Náhledu.)
Zjednodušená metoda pro výpočet účinků druhého řádu by se měla použít po lineárním výpočtu. Tato metoda je v programu SCIA Engineer založená na jmenovité křivosti podle EN 1992-1-1, čl. 5.8.8. Pro použití zjednodušené metody musí být splněna následující podmínky:
Jsou spočteny vnitřní síly s účinky druhého řádu - pokud je štíhlost sloupu vyšší než limitní štíhlost (viz kapitola Posudek štíhlosti) . Tyto síly jsou zobrazeny ve funkci Vnitřní síly (strom Pokročilý beton), viz kapitola Posudek vnitřních sil. Podrobný postup pro výpočet účinků druhého řádu je popsána v kapitole Výpočet jmenovitého momentu druhého řádu.
Pokud jsou vnitřní síly vypočteny s použitím nelineárního výpočtu a jsou použity servisy ve stromu Pokročilý beton, pak zaškrtávací políčko Použít data vzpěru v řešiči pro beton (kapitola Data o vzpěru) nebo v datech betonového dílce (kapitola Skupina Výpočet sloupu) musí být vypnuto, protože by se účinky druhého řádu jinak počítaly dvakrát (obecnou metodu a také zjednodušenou metodou)
V tabulce je provedeno porovnání obecné a zjednodušené metody pro jeden sloup jednoduchého rámu o dvou polích (příklad Tutorial_column_01.esa)
| Model konstrukce |  |
|
| Metoda | ||
| Nastavení projektu | 
|
Všechny nelinearity jsou vypnuty |
| FNL data | 
|
Žádné |
| Kombinace | 
|
|
| Dotvarování | fef = f = 2.5 | fef = f = 2.5 |
| Pracovní diagram betonu | 
|
|
| Pracovní diagram nepředpjaté výztuže | 
|
|
| Data o vzpěru |
Lineární stabilita ky = 1,15
|
Lineární stabilita ky = 1,15
|
| Vnitřní síly |
Vnitřní síly ve stromu Výsledky pro nelineární kombinaci NC3
|
Vnitřní síly ve stromu Výsledky pro nelineární kombinaci NC3 Vnitřní síly ve stromu Pokročilý beton pro nepředpjatý posudek podle MSÚ a lineární kombinaci C01
|
| Posudek sloupu | 
|
Všechny funkce ve stromu Pokročilý beton
|
Největší moment ve sloupu B2 bez účinků druhého řádu a imperfekcí je v hlavě sloupu a hodnota je - 69,14 kN/M. Pro obecnou metodu, je ohybový moment v hlavě s účinky druhého řádu a imperfekcí roven -96,59, to znamená 1,39 násobné zvýšení. Pro zjednodušenou metodu, je ohybový moment v hlavě s účinky druhého řádu a imperfekcí roven -145,31, to znamená 2,10 násobné zvýšení. Z toho vyplývá, že použití obecné metody vede k hospodárnějšímu návrhu.
