

|
||
|
|
||
Výpočet momentu prvního řádu probíhá podle následujícího postupu:
Excentricita prvního řádu bez vlivu imperfekcí se vypočte podle vzorce

kde
e1,y(z) excentricita prvního řádu ve směru osy y (z) lokálního souř. systému
M0Ed,y(z) moment prvního řádu kolem lokální osy y (z) (v programu označen jako My(z))
NEd je návrhová osová síla ve spočtených řezech sloupu (v programu hodnota N)
e0e,y(z) ekvivalentní excentricita prvního řádu ve směru osy y (z) lokálního souř. systému
M0e,y(z) ekvivalentní moment prvního řádu kolem osy y (z) lokálního souř. systému
N0,e ekvivalentní osová síla
ekvivalentní moment prvního řádu se spočte podle čl. 5.8.8,2 (2) EN 1992-1-1.
M0,ey = max (0,6*M02,y +0,4*M01,y; 0,4* M02,y)
M0,ez = max (0,6*M02,z +0,4*M01,z; 0,4*M02,z)
kde
M01y(z) toto je první koncový ohybový moment kolem lokální osy y (z) s menší absolutní hodnotou než druhý koncový ohybový moment. | M01y(z) |< | M02y(z) | Stejné hodnoty se použijí pro výpočet limitní štíhlosti.
M02y(z) toto je druhý koncový ohybový moment kolem lokální osy y (z) s větší absolutní hodnotou než první koncový ohybový moment. | M02y(z) |≥ | M01y(z) | Stejné hodnoty se použijí pro výpočet limitní štíhlosti.
Ekvivalentní osová síla se vypočítává podle stejných pravidel jako ekvivalentní ohybové momenty
N0,e = max (0,6*N02 +0,4*N01; 0,4*N02)
kde
N01 Toto je první koncová osová síla s absolutní hodnotu menší než osová síla na druhém konci. |N01|< |N02|.
N02 Toto je druhá koncová osová síla s absolutní hodnotu větší než osová síla na prvním konci. |N01|< |N02|.
Ekvivalentní hodnoty ohybových momentů a osové síly jsou stejné ve všech řezech na sloupu a hodnoty ekvivalentní excentricity a ekvivalentních ohybových momentů lze zobrazit v číselném výstupu po přidání vybraných hodnot do tabulky (ikonou Editor tabulek  v Náhledu)
v Náhledu)
Imperfekce jsou v programu reprezentovány sklonem podle bodu 5.2 (5) EN 1992-1-1. Sklon se spočte kolem obou lokálních os (y a z) podle vzorce:
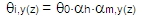
kde
F0 je základní hodnota sklonu. Hodnota je národní parametr, to znamená, že může být pro jednotlivé země rozdílná. Hodnota může být nastavena v Nastavení betonu (Správce národních příloh > EN 1992-1-1 > Obecné > MSÚ > Obecné > Theta_0 )
αh je redukční součinitel pro délku sloupu nebo výšku konstrukce. Hodnota se vypočte podle vzorce
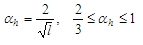
αm,y(z) je redukční součinitel pro počet dílců spočtený podle vzorce
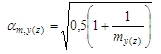
je délka sloupu nebo výška konstrukce zadaná v parametru Celk. výška na záložce Data o vzpěru v dialogu Vzpěrné a relativní délky (vlastnosti dílce > parametr Vzpěrné a relativní délky > tlačítko Upravit), viz kapitola >
my(mz) je počet svislých dílců přispívajících k celkovému vlivu imperfekce kolmé k lokální ose y(z). To znamená, že hodnota se použije pro přepočet ohybového momentu kolem lokální osy y(z). Toto je hodnota zadaná na záložce Data o vzpěru v dialogu Vzpěrné a relativní délky (vlastnosti dílce > parametr Vzpěrné a relativní délky > tlačítko Upravit)
Vliv imperfekce pro samostatný sloup a také pro konstrukci se vždy zohlední jako excentricita podle čl. 5.2 (7a) EN 1992-1-1 . V prvním kroku se spočte základní excentricita od imperfekce v obou směrech lokálních os a to podle vzorce
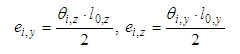
kde
Fi,y(z) je náklon kolem lokální osy y(z) (kolmo k lokální ose y(z))
l0,y(z) je efektivní délka dílce (sloupu) kolem lokální osy y(z) (kolmo k lokální ose y(z)), kterou lze zadat v Datech prutu o vzpěru, kapitola Datea prutu o vzpěru.
Ve druhém kroku se základní hodnota excentricity od imperfekce kolem obou lokálních os přepočte v závislosti na štíhlosti a excentricitách prvního řádu:
kde
e1,y(z) excentricita prvního řádu ve směru osy y (z) lokálního souř. systému (viz kapitola Výpočet excentricity prvního řádu bez účinku imperfekcí)
ei,1 je excentricita způsobená imperfekcí přepočítanou do směru výsledné excentricity prvního řádu ei,1 = ei,y·cos(α)+ ei,z·sin(α). Pro zjednodušení se v programu hodnota ei,1 spočítá podle vzorce: ei,1 = max(ei,y;ei,z)
α je úhel mezi směrem výsledné excentricity prvního řádu a lokální osou y
Konečná hodnota excentricity od imperfekcí se vypočte podle vzorce uvedeného níže a je uvedena v číselném výstup pro hodnotu
My,přepoč a Mz,přepoč
ei,y = max(ei,y,1; ei,y,2)
ei,z = max(ei,z,1; ei,z,2)
Tabulka přepočtené a konečné excentricity způsobené imperfekcí pro různé hodnoty štíhlosti a excentricit první řádu podle zadaných hodnot a předchozích vzorců je uvedena níže (příklad tutorial_column_02.esa)
| Typ | Sloup | B1 | B2 | B3 | B4 | B5 | B6 | B7 |
| Základní | ei,y [mm] | 9 | 9 | 9 | 9 | 9 | 9 | 9 |
| ei,z [mm] | 9 | 9 | 9 | 9 | 9 | 9 | 9 | |
| e1,y [mm] | 50 | 0 | 50 | 50 | 0 | 50 | 50 | |
| e1,z [mm] | 50 | 50 | 0 | 50 | 50 | 0 | 50 | |
| štíhlost | ly = lz | ly < lz | ly < lz | ly < lz | ly > lz | ly > lz |
ly > lz |
|
| Přepočtené | ei,y,1 [mm] | 9 | 9 | 9 | 9 | 0 | 0 | 0 |
| ei,z,1 [mm] | 9 | 0 | 0 | 0 | 9 | 9 | 9 | |
| ei,y,2 [mm] | 9 | 0 | 9 | 6 | 0 | 9 | 6 | |
| ei,z,2 [mm] | 9 | 9 | 0 | 6 | 9 | 0 | 6 | |
| Konečný | ei,y [mm] | 9 | 9 | 9 | 9 | 0 | 9 | 6 |
| ei,z [mm] | 9 | 9 | 0 | 6 | 9 | 9 | 9 |
Výsledky spočtené programem jsou následující:
Směr (znaménko) konečné hodnoty excentricity způsobené imperfekcí musí být stejný jako směr (znaménko) excentricity prvního řádu.
Excentricita prvního řádu včetně vlivu imperfekcí se vypočte podle vzorce
eo,y(z) = e1,y(z) + ei,y(z) > e0,min,y(z)
Minimální excentricita prvního řádu se podobné jako excentricita způsobená imperfekcí vypočítá ve směru obou lokálních os podle vzorce:
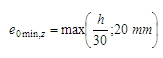
kde
e1,y(z) excentricita prvního řádu ve směru osy y (z) lokálního souř. systému (viz kapitola Výpočet excentricity prvního řádu bez účinku imperfekcí)
ei,y(z) je excentricita prvního řádu způsobená imperfekcí ve směru osy y (z) lokálního souř. systému (viz kapitola Výpočet excentricity od imperfekcí)
e0,min,y(z) je minimální excentricita prvního řádu ve směru lokální osy y (z) podle čl. 6.1 (4) EN 1992-1-1. Tato minimální hodnota budou uvažována pouze v případě , že políčko Zohlednit výstřednost podle 6.1.4 bude zaškrtnuto (Řešič pro betonové konstrukce > Obecné > Výpočet > Sloup > Pokročilé nastavení), viz kapitola Zohlednit výstřednost podle 6.1.4
b je maximální šířka průřezu (maximální rozměr průřezu ve směru lokální osy y)
h je výška průřezu (rozměr průřezu ve směru lokální osy z)
Po výpočtu excentricity prvního řádu včetně vlivu imperfekce, se spočte moment prvního řádu včetně vlivu imperfekce kolem lokální osy y (z):
M0Ed,y(z) = NEd* eo,z(y)
Tabulka přepočtené a konečné excentricity druhého řádu pro různé hodnoty excentricit první řádu podle zadaných hodnot a předchozích vzorců je uvedena níže (příklad tutorial_column_03.esa)
| Typ |
Sloup b/h =400/700 mm |
B1 (x=0) |
B1 (x=1,8) |
B2 (x=0) |
B2 (x=1,8) |
B3 (x=0) |
B3 (x=1,8) |
| Základní | M0Ed,z/NEd [mm] | -50 | 0 | 0 | 0 | -50 | 0 |
| M0Ed,y/NEd [mm] | -50 | 0 | -50 | 0 | 0 | 0 | |
| e0e,y[mm] | 20 | 0 | 20 | ||||
| e0e,z[mm] | 20 | 20 | 0 | ||||
| e1,y [mm] | -50 | 20 | 0 | 0 | -50 | 20 | |
| e1,z [mm] | -50 | 20 | -50 | 20 | 0 | 0 | |
| Přepočtené | ei,y [mm] | -9 | 9 | 9 | 9 | -9 | 9 |
| ei,z [mm] | -6 | 6 | -9 | 9 | 0 | 0 | |
| e0,min,y [mm] | -20 | 20 | 20 | 20 | -20 | 20 | |
| e0,min,z [mm] | -23 | 23 | -23 | 23 | 23 | 23 | |
| Konečný | e0,y [mm] | -59 | 29 | 20 | 20 | -59 | 29 |
| e0,z [mm] | -56 | 26 | -59 | 29 | 23 | 23 | |
Výsledky spočtené programem jsou následující:
• Moment prvního řádu a excentricita s vlivem imperfekce jsou uvedeny v číselném výstup pro hodnoty My přepoč a Mz přepoč.
• Směr (znaménko) minimální hodnoty excentricity musí být stejný jako směr (znaménko) excentricity prvního řádu.
Jmenovitý moment druhého řádu se spočte podle čl. 5.8.8.2 (3) EN 1992-1-1.
M2,y(z) = NEd* e2,z(y)
kde
NEd je návrhová osová síla ve spočtených řezech sloupu (v programu hodnota N)
e2,z(y) je excentricita prvního řádu ve směru osy z (y) lokálního souř. systému
Základní hodnota excentricity druhého řádu se zohlední pouze tehdy, pokud:
Základní hodnoty excentricity druhého řádu se vypočítávají podle vzorce uvedeného níže v prvním kroku:
| lz >lz,lim | zaškrtávací políčko Použít data o vzpěru | Excentricita 2. řádu |
| Ano | Zapnuto | e2,y = (1/r)z.l0,z2 / cz |
| Ano | Vypnuto | e2,y = 0 |
| NE | Zapnuto | |
| Ne | Vypnuto | |
| ly >ly,lim | zaškrtávací políčko Použít data o vzpěru | Excentricita 2. řádu |
| Ano | Zapnuto | e2,z = (1/r)y.l0,y2 / cy |
| Ano | Vypnuto | e2,z = 0 |
| NE | Zapnuto | |
| Ne | Vypnuto |
kde
(1/r)y(z) je křivost kolem lokální osy y (z) (kolmo na lokální osu y (z)) vypočítané podle čl. 5.8.8.3 v EN 1992-1-1
l0,y(z) je efektivní délka dílce (sloupu) kolem lokální osy y(z) (kolmo k lokální ose y(z)), kterou lze zadat v Datech prutu o vzpěru, kapitola Datea prutu o vzpěru.
cy(z) je součinitel závislý na průběhu křivosti kolem lokální osy y (z) podle čl. 5.8.8.2 (4) EN 1992-1-1.
cy(z) = 8 (pro moment prvního řádu konstantní po celé délce sloupu kolem lokální osy y(z))
cy(z) = 10 (pro ostatní případy)
ly(z) je štíhlostní poměr kolem lokální osy y(z)
ly(z),lim je limitní štíhlostní poměr kolem lokální osy y(z)
Ve druhém kroku se základní hodnota excentricity druhého řádu ve směru lokálních obou os přepočte v závislosti na štíhlosti a excentricitách prvního řádu:
- ve směru osy z
e2,z,1 = e2,z .... pokud ly ≤ lz
e2,z,1 = 0m .... pokud ly > lz
kde
e1,y(z) excentricita prvního řádu ve směru osy y (z) lokálního souř. systému (viz kapitola Výpočet excentricity prvního řádu bez účinku imperfekcí)
ei,1 je excentricita druhého řádu přepočítaná do směru výsledné excentricity prvního řádu ei,1 = e2,y·cos(α)+ e2,z·sin(α). Pro zjednodušení se v programu hodnota ei,1 spočítá podle vzorce: ei,1 = max(e2,y;e2,z)
α je úhel mezi směrem výsledné excentricity prvního řádu a lokální osou y
Konečná hodnota excentricity od imperfekcí se vypočte podle vzorce uvedeného níže a je uvedena v číselném výstup pro hodnotu My,přepoč a Mz,přepoč.
e2,y = max(e2,y,1; e2,y,2)
e2,z = max(e2,z,1; e2,z,2)
Tabulka přepočtené a konečné excentricity druhého řádu pro různé hodnoty štíhlosti a excentricit první řádu podle zadaných hodnot a předchozích vzorců je uvedena níže (příklad tutorial_column_02.esa)
| Typ | Sloup | B1 | B2 | B3 | B4 | B5 | B6 | B7 |
| Základní | e2,y [mm] | 22 | 22 | 22 | 22 | 22 | 22 | 22 |
| e2,z [mm] | 22 | 22 | 22 | 22 | 22 | 22 | 22 | |
| e1,y [mm] | 50 | 0 | 50 | 50 | 0 | 50 | 50 | |
| e1,z [mm] | 50 | 50 | 0 | 50 | 50 | 0 | 50 | |
| štíhlost | ly = lz | ly < lz | ly < lz | ly < lz | ly > lz | ly > lz |
ly > lz |
|
| Přepočtené | e2,y,1 [mm] | 22 | 22 | 22 | 22 | 0 | 0 | 0 |
| e2,z,1 [mm] | 22 | 0 | 0 | 0 | 22 | 22 | 22 | |
| e2,y,2 [mm] | 22 | 0 | 22 | 15 | 0 | 22 | 15 | |
| e2,z,2 [mm] | 22 | 22 | 0 | 15 | 22 | 0 | 15 | |
| Konečný | e2,y [mm] | 22 | 22 | 22 | 22 | 0 | 22 | 15 |
| e2,z [mm] | 22 | 22 | 0 | 15 | 22 | 22 | 22 |
Výsledky spočtené programem jsou následující:
Směr (znaménko) konečné hodnoty excentricity druhého řádu musí být stejný jako směr (znaménko) excentricity prvního řádu.
Křivost pro výpočet excentricity druhého řádu se vypočte podle čl. 5.8.8.3 v EN 1992-1-1.
(1/r)y(z) = Kr*Kf,y(z)*(1/r0)y(z)
kde
Kr je opravný součinitel závislý na osovém zatížení, viz čl. 5.8.8.3 (3) EN 1992-1-1. Tento součinitel závisí na relativní normálové síle (n) a mechanické poměru vyztužení ().
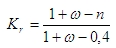
Kf,y(z) je součinitel zohledňující dotvarování kolem lokální osy y (z) podle čl. 5.8.8.3 (4) in EN 1992-1-1. Tento součinitel závisí na efektivním poměru dotvarování (ef) a součiniteli (y(z)) závislém na štíhlosti
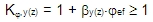
(1/r0)y(z) je základní hodnota křivosti kolem lokální osy y (z). Tato hodnota závisí na účinné výšce průřezu a přetvoření výztuže při dosažení návrhové meze kluzu ve výztuži

Z toho vyplývá, že výpočet křivosti závisí na mnoha parametrech a součinitelích, z nichž nejdůležitější jsou tyto:
Relativní osová síla
Relativní normálová síla se používá pro výpočet opravného součinitele Kr vypočte se podle vzorce
n = NEd / Ac•fcd
kde
NEd je návrhová hodnota působící tlakové osové síly v počítaném průřezu
Ac je průřezová plocha betonu
fcd je návrhová hodnota pevnosti betonu v tlaku
Procento mechanické výztuže
Procento mechanické výztuže, které se používá pro výpočet opravného součinitele Kr, závisí na celkové ploše podélné výztuže. Z toho vyplývá, že pro návrh výztuže do sloupu a pro posudek sloupu se zohledňuje jiné procento mechanické výztuže.
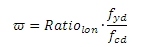
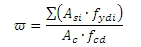
kde
poměrlon je procento výztuže načtené z nastavení betonu (Řešič pro betonové konstrukce > Obecné > Výpočet > Sloup > Pokročilé nastavení > Uživatelský odhad stupně vyztužení pro návrh výztuže), viz kapitola Uživatelský odhad stupně vyztužení pro návrh výztuže
fyd je návrhová mez kluzu výztuže Třída výztuže se zadává v Datech projektu nebo, jsou-li na posuzovaném sloupu zadána data betonového dílce, v datech betonového dílce (viz kapitola 4.2.34.2.4)
fcd je návrhová hodnota pevnosti betonu v tlaku
Asi je průřezová plocha i-té výztuže v průřezu zadaná přes Redes nebo jako volné pruty
fydi je návrhová mez kluzu i-té výztuže v průřezu zadané přes Redes nebo jako volné pruty
Efektivní poměr dotvarování
Pro výpočet součinitele Kf,y(z) se používá poměr dotvarování načtený z nastavení betonu (pokud nejsou na sloupu definována data dílce) nebo z dat betonového dílce. To znamená, že pokud chce uživatel zohlednit efektivní poměr dotvarování podle čl. 5.8.4 v EN 1992-1-1, hodnota tohoto poměru dotvarování musí být přímo zadána v nastavení betonu nebo v datech betonového dílce. V opačném případě se uvažuje konečný poměr dotvarování.
| Řešič pro betonové konstrukce > SLS > Dotvarování | Data betonového dílce |
|
|
Štíhlost
Štíhlost sloupu pro výpočet součinitele Kf,y(z) se uvažuje parametrem (by(z)) , který se vypočte podle vzorce : 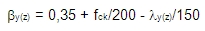
kde
fck je charakteristická hodnota pevnosti betonu v tlaku
ly(z) je štíhlostní poměr kolem lokální osy y(z)
Účinná výška průřezu
Účinná výška průřezu se používá pro výpočet základní hodnoty křivosti a spočte se podle čl. 5.8.8.3 (2) EN 1992-1-1.

kde
isy(z) je poloměr setrvačnosti celkové plochy výztuže ve směru lokální osy y(z)
b je maximální šířka průřezu (maximální rozměr průřezu ve směru lokální osy y)
h je výška průřezu (rozměr průřezu ve směru lokální osy z)
Poloměr setrvačnosti celkové výztuže závisí na zvolené možnosti v položce Typ posudku (strom Pokročilý beton > 1D dílec > Vnitřní síly). To znamená, že poloměr setrvačnosti celkové výztuže může být jiný pro návrh výztuže sloupu a pro posudek sloupu. Výpočet pro návrh výztuže sloupu závisí na typu metody a tvaru betonového průřezu. Existují následující metody pro výpočet poloměr setrvačnosti celkové výztuže:
- moment setrvačnosti plochy výztuže
- poloměr setrvačnosti celkové plochy výztuže
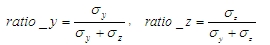
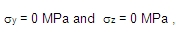 pak
pak 
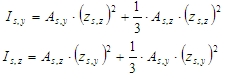
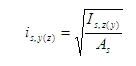
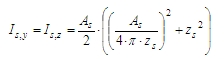
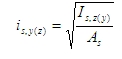
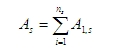
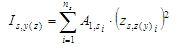
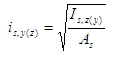
kde
poměrlon je procento výztuže načtené z nastavení betonu (Řešič pro betonové konstrukce > Obecné > Výpočet > Sloup > Pokročilé nastavení > Uživatelský odhad stupně vyztužení pro návrh výztuže), viz kapitola Uživatelský odhad stupně vyztužení pro návrh výztuže
Ac je průřezová plocha betonu
ns Je počet prutů v průřezu (počet prutů pro variantu Pouze návrh rohů závisí na tvaru průřezu, viz kapitola Pouze návrh rohů)
A1si je průřezová plocha i-tého prutu výztuže
zs,y(z)i je poloha i-tého prutu výztuže od těžiště betonového průřezu ve směru lokální osy y (z) (pozice prutů pro variantu Pouze návrh rohů závisí na tvaru průřezu, viz kapitola Pouze návrh rohů)
sy(z) je ohybové napětí v betonu vypočtené pro betonový průřez neporušený trhlinami podle vzorce: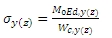
M0Ed,y(z) je moment prvního řádu kolem lokální osy y (z) (v programu označen jako My(z)) bez imperfekcí
Wc,y(z) je modul průřezu betonového průřezu kolem lokální osy y (z).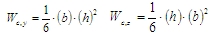
zs,y(z) je poloha výztuže od těžiště betonového průřezu ve směru osy y (z) pro obdélníkový průřez (pozice prutů pro variantu Pouze návrh rohů závisí na tvaru průřezu, viz kapitola Pouze návrh rohů)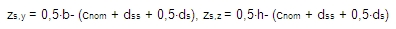
zs je poloha výztuže od těžiště betonového průřezu pro kruhové průřezy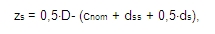
b je šířka obdélníkového průřezu
h je výška obdélníkového průřezu
D je průměr kruhového průřezu
cnom je jmenovité krytí výztuže načtené z nastavení betonu (Výchozí nastavení návrhu) nebo z dat betonového dílce, pokud jsou tato na počítaném sloupu zadána
ds je průměr podélné výztuže načtený z nastavení betonu (Výchozí nastavení návrhu) nebo z dat betonového dílce, pokud jsou tato na počítaném sloupu zadána
dss je průměr příčné výztuže (třmínků) načtený z nastavení betonu (Výchozí nastavení návrhu) nebo z dat betonového dílce, pokud jsou tato na počítaném sloupu zadána
V následující tabulce je ukázán výpočet účinné výšky průřezu pro různé typy posudku, různé průřezy a různé metody
Uživatelem zadaná (skutečná) výztuž definovaná prostřednictvím Redes a volných prutů není při výpočtu účinné výšky průřezu pro návrh výztuže sloupu uvažována (Typ posudku = Návrh MSÚ ve funkci vnitřní síly)
Výpočet přetvoření ve výztuži při dosažení návrhové meze kluzu
Přetvoření ve výztuži při dosažení návrhové meze kluzu výztuže se používá pro výpočet základní hodnoty křivosti. Tato hodnota závisí na materiálových vlastnosti výztuže. Z toho vyplývá, že pro návrh výztuže do sloupu a pro posudek sloupu se zohledňuje jiná hodnota.
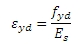
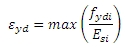
kde
fyd je návrhová mez kluzu výztuže Třída výztuže se zadává v Datech projektu nebo, jsou-li na posuzovaném sloupu zadána data betonového dílce, v datech betonového dílce (viz kapitola Skupina Návrh a Skupina Výpočet sloupu)
Es je návrhová hodnota modulu pružnosti výztuže Třída výztuže se zadává v Datech projektu nebo, jsou-li na posuzovaném sloupu zadána data betonového dílce, v datech betonového dílce (viz kapitola Skupina Návrh a Skupina Výpočet sloupu)
fydi je návrhová mez kluzu i-té výztuže v průřezu zadané přes Redes nebo jako volné pruty
Esi je návrhová hodnota modulu pružnosti i-té výztuže v průřezu zadané přes Redes nebo jako volné pruty