|
||
|
|
||
The basic cross-section characteristics are calculated using the standard formulas from solid mechanics. For detailed information, reference is made to Ref.[3] and Ref.[4].
The cross-section is discretized into n elemental areas dA.
First, using the arbitrary origin of the UCS or 'Input' Axis system the following properties are calculated using a horizontal Y-axis and a vertical Z-axis:
Using these magnitudes the coordinates of the centroid are determined:
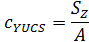
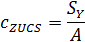
The centroid defines the origin of the LCS Axis system with YLCS and ZLCS axis parallel to the axis of the UCS system. According to these axis the second moments of area can be determined:
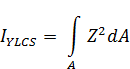
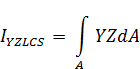
Finally, using these magnitudes the Principal Axis system and corresponding characteristics can be determined:
Second Moment of Area:
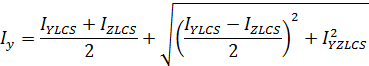
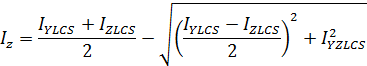
Angle of Rotation:
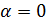in case 
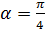in case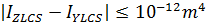 
and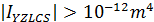 
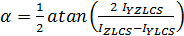otherwise
The above determination of the angle of rotation accounts for minor numerical discrepancies. For background information, reference is made to Ref.[1].
In addition, in case the angle of rotation is calculated according to the above formula and exceeds a tolerance of 3°, the angle is increased by π/2 in case Iz > Iy.
In case of multi-material cross-sections the basic characteristics are determined using the principles given in this paragraph. For background information see Ref.[5]
First the area Ai and centroid position of each cross-section part/polygon i are calculated.
To determine the location of the centroid (Neutral Axis 'NA') of the whole cross-section the following general equation is used:
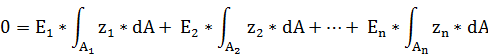
Where n represents the number of polygons and Ei the E-modulus of the material of the respective polygon.
The distances z1, z2, … zn are the distances from the NA to the centroid of each polygon (measured in the UCS Axis system). These distances can be written in function of the centroid distance cZUCS so the above equation can be solved this centroid distance.
The above equation illustrates the principle used for cZUCS, in the same way the equation can be written out for cYUCS.
The Area of the multi-material section is calculated using the following general formula:
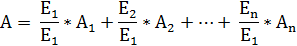
Where n represents the number of polygons, Ei the E-modulus of the material of the respective polygon and Ai the area of the respective polygon.
As indicated by the equation, each polygon of the multi-material cross-section is in fact referenced to the material of the 'first' polygon.
Within SCIA Engineer this literally means the 'first' inputted polygon. So the material of this 'first' inputted polygon serves as reference material for the multi-material cross-section. This 'first' material is shown with a cyan background color for easy reference.
The Second Moment of Area of the multi-material section is calculated using the following general formula:
Where n represents the number of polygons, Ei the E-modulus of the material of the respective polygon and Ai the area of the respective polygon.
As indicated by the equation, each polygon of the multi-material cross-section is in fact referenced to the material of the 'first' polygon.
The above equation is used to determine IYLCS, IZLCS and IYZLCS.