

|
||
|
|
||
All dynamic computations can be related to the solution of the equations of dynamic equilibrium which can be written in matrix form:
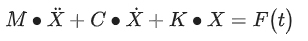
|
(1.1) |
When this matrix equation is compared to the equation of static equilibrium:
|
|
(1.2) |
It is clear that the dynamic equation of equilibrium requires more data than the static equation. In fact, we have to supply sufficient information to compute:
C :The damping matrix
F(t) : The solicitation as a function of time
The results that are obtained when solving the equation include displacements as a function of time as well as velocity, acceleration and internal forces. The amount of results can therefore become exhaustive. The methods available to solve equation (1.1) are mostly based on a modal superposition principle. The assumption is made that the behaviour of the structure can be obtained by superposing a number of natural deformation modes each multiplied by a weighing factor that depends on the solicitation. These natural modes or eigenmodes are obtained from the solution of:
|
|
(1.3) |
The eigenvalues and eigenvectors can be used for further dynamic studies. Four different types of dynamic computations are allowed presently in SCIA Engineer:
Harmonic solicitation
Spectral analysis
Direct time integration
Von Karman vortices