Open topic with navigation

Material

The material library includes several concrete and reinforcement classes specifically according to NBR 6118/2014 and NBR 7480/2007. Generally, there are the following concrete and reinforcement classes:

Concrete library

Concrete library looks as follows and it has the following properties:

Name

name of the concrete grade

Code independent

list of the characteristic which are general for all codes but calculated dependent on the code. The most important for calculation are the following

E_cs concret secant modulus

calculated according to chapter 8.2.8 from NBR 6118/2014

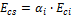
Where:

E_ci concret initial modulus – calculated according to chapter 8.2.8 from NBR 6118/2014

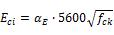
	for fck between 20 and 50 MPa
	for fck between 55 and 90 MPa

α_E

see item type of aggregate below

Basalt and diabase
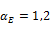
Granite and gneiss
Calcareous
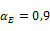
Sandstone

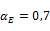
Poison coefficient

ν = 0,2 according to chapter 8.2.9 from NBR 6118/2014

G modulus

this items is calculated according to chapter 8.2.9 from NBR 6118/2014 when checkbox Independent G modulus is switched OFF

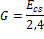
Code dependent

these characteristics are specific for the code and there are the following:

Characteristic compressive cylinder strength (f_ck)

according to concrete class

Calculate dependent values

if this checkbox is ON then all values below are calculated according to NBR

Mean tensile strength (f_ctm)

based on the f_ck - calculated according to chapter 8.2.5 from NBR 6118/2014

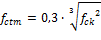
	for concrete fck<=50MPa
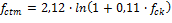
	for fckbetween 55 and 90 MPa

f_ctk,inf

lower value of f_ctk

f_ctk,inf = 0.7 * f_ctm

f_ctk,sup

upper value of f_ctk

f_ctk,sup = 1.3 * f_ctm

Design compressive strength – regular

calculated according to Table 12.1 from NBR 6118/2014

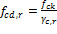
Design compressive strength – special

calculated according to Table 12.1 from NBR 6118/2014

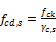
Design compressive strength – exceptional

calculated according to Table 12.1 from NBR 6118/2014

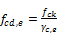
Concrete shortening strain at the beginning of the plastic plateau ε_c2

calculated according to chapter 8.2.10.1 from NBR 6118/2014

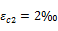
	for concrete fck<=50MPa
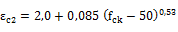
	for fckbetween 55 and 90 MPa

Concrete shortening ultimate strain ε_cu

calculated according to chapter 8.2.10.1 from NBR 6118/2014

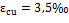
	for concrete fck<=50MPa
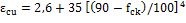
	for fckbetween 55 and 90 MPa

Stone diameter

Type of aggregate

this value affects the calculation of modulus of elasticity (E_cs)

Basalt and diabase
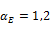
Granite and gneiss
Calcareous
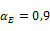
Sandstone

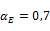
Stress-strain diagram

only parabola-rectangular is available - according to chapter 8.2.10.1 from NBR 6118/2014

σ_c = 0,85 * f_cd * [1 – (1 – ε_c/ε_c2)ⁿ]

For f_ck = 50MPa : n = 2

For f_ck > 50MPa : n = 1,4 + 23,4 * [(90 – f_ck) / 100]⁴

Reinforcement library

Reinforcement library looks as follows and it has the following properties:

Name

name of the reinforcement grade

Code independent

list of the characteristic which are general for all codes but calculated dependent on the code. The most important for calculation are the following

E modulus

- according to chapter 8.3.5 from NBR 6118/2014

Poison coefficient

ν = 0,2 - according to chapter 8.2.9 from NBR 6118/2014

G modulus

this items is calculated according to chapter 8.2.9 from NBR 6118/2014 when checkbox Independent G modulus is switched OFF

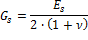
Bar surface

this property is different per reinforcement grade according to Table 8.3 from NBR 6118/2014

CA-25 – smooth (not editable)

CA-50 – ribbed (not editable)

CA-60 – smooth/ribbed/indented

Code dependent

these characteristics are specific for the code and there are the following:

Characteristic yield strength (f_yk)

according to reinforcement class

Calculate dependent values

if this checkbox is ON then all values below are calculated according to NBR

Design yield strength – regular

calculated according to Table 12.1 from NBR 6118/2014

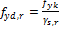
Design yield strength – special

calculated according to Table 12.1 from NBR 6118/2014

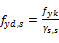
Design yield strength – exceptional

calculated according to Table 12.1 from NBR 6118/2014

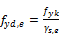
Ultimate steel elongation strain

ε_u = 10 ‰

Stress-strain diagram

only bilinear without inclined top branch is available

Open topic with navigation