

|
||
|
|
||
Difference between mean strain in the reinforcement and the mean strain in concrete between the cracks is calculated according to EN 1992-1-1, formula 7.9
where
| σs | the stress in the most tensioned reinforcement |
| Es | design value modulus of elasticity of the most tensioned reinforcement member |
| kt | |
| fct,eff | is the mean value of the tensile strength of the concrete effective at the time when the cracks may first be expected to occur.The value can be set by "Type of strength for calculation of cracking forces" |
| ρp,eff | ratio of reinforcement within effective area of concrete in tension |
| αe | ratio of design value of modulus of elasticity of the most tensioned reinforcement and modulus elasticity of the concrete |
From the formula above follows that difference between mean strain in the reinforcement and concrete mainly depends on:
Strain in the most tensioned reinforcement is calculated according to formula below
There are used following preconditions in SCIA Engineer:
| Linear stress-strain diagram of concrete | Linear stress-strain diagram of reinforcement |
|---|---|
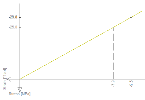
|

|
The tension stiffening effect represents the capacity of the intact concrete between neighbouring cracks to carry a limited amount of tensile forces. The reason for this effect is bond slip between the reinforcement and the neighbouring concrete. The decreasing of stress in reinforcement due to tension stiffening can be calculated according to formula:
where
| kt |
factor dependent on duration of the load. The following values should be used according to code EN 1992-1-1, chapter 7.3.4(2).
The value of kt in SCIA Engineer depends on type of load. It is calculated according followed formula. kt = kt,long + (kt,short - kt,long) ∙ (1 - Coefflong)
|
| fct,eff |
is the mean value of the tensile strength of the concrete effective at the time. When the cracks may first be expected to occur.The value can be set by "Type of strength for calculation of cracking forces". |
| ρp,eff |
ratio of reinforcement within effective area of concrete in tension. This ratio is calculated only for non-prestressed reinforcement (prestressed reinforcement is not taken into account for check crack width) according to formula
|
| As,eff | area of non-prestressed reinforcement (see chapter 4.4) within effective area of concrete in tension |
| Ac,eff | the effective area of concrete in tension surrounding the reinforcement. This is area of reinforcement bounded by line, which is in distance hc,eff from the most tensioned fibre of concrete in direction of bending moment resultant |
| hc,eff |
the depth of effective area of concrete in tension surrounding the reinforcement.
|
| h | the height of cross-section in direction of resultant of the bending moments (thickness of FEM element in centroid) |
| d | effective depth of cross-section in direction of resultant of the bending moments |
| x | depth of concrete in compression calculated for uncracked section with taking into account conditions in code chapter 4.6.1.1. |
| αe |
ratio of design value of modulus of elasticity of the most tensioned reinforcement and modulus elasticity of the concrete
|
| Es | design value of modulus of elasticity of the most tensioned The value is loaded from material properties of the reinforcement, see picture below |
| Ec | modulus of elasticity of concrete. The value is loaded from material properties of the concrete |
The program finishes with error if area of non-prestressed reinforcement As,eff is zero,
EN 1992-1-1 does not give instruction, how creep under varying load should be taken into account for calculation of the crack width. The creep can be generally taken into account by assuming that effective module of elasticity (EN 1992-1-1, clause 5.8.7(2) ) for calculation modular ratio (Es/Ec,eff ≈ 15). A Lower value of modular ratio (greater value of module of elasticity of concrete than effective ) may be used where less than 50 % of the stresses arise from quasi-permanent load. The effective module of elasticity van be taken into account by check box Use effective modulus of concrete (see 2.1.3 ) .The different value of modulus of elasticity can be input directly in material properties, but these changes has influence to FEM analysis too.