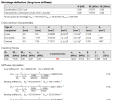
Calculation curvature, strain and stiffness caused by shrinkage of 1D element
Calculation shrinkage forces
The forces caused by shrinkage are calculated according to formulas below. The forces are calculated for both states: uncracked and cracked cross-section.
Nshr = -ecs(t,ts)·CoefReinfå(Esi·Asi)
Mshr,y = Nshr·eshr,z
Mshr,z = Nshr·eshr,y
where
eshr,y =å(Esi·Asi)/ å(Esi·Asi·ysi) - tiy
eshr,z =å(Esi·Asi)/ å(Esi·Asi·zsi) - tiz
-ecs(t,ts)· - is total shrinkage strain, see "Parameters for calculation of shrinkage strain"
Coefreinf is coefficient increasing amount of reinforcement, see "Coefficient for increasing amount of reinforcement"
Esi - is modulus of elesticity of i-th bar of reinforcement
Asi - is area of reinforcement of i-th bar of reinforcement
ysi – position of i-th bar of reinforcement from centre of gravity of cross-section in y-direction
zsi – position of i-th bar of reinforcement from centre of gravity of cross-section in z-direction
tiy – distance between centre of gravity transformed uncracked/cracked cross-section and centre of gravity of concrete cross-section in y-direction
tiz – distance between centre of gravity transformed uncracked/cracked cross-section and centre of gravity of concrete cross-section in z-direction
The forces caused by shrinkage are presented in detailed output in chapter Shrinkage deflection (long-term stiffness). Presented forces are calculated for uncracked cross-section
Calculation strain and curvature caused by the shrinkage
Strain and curvature caused by shrinkage are calculated for each 1D elements and these value are calculated for both state (uncracked and cracked cross-section)
Calculation strain caused by shrinkage:
ex =-ecs(t,ts)·CoefReinf·å(Esi·Asi)/(Eceff·Ai)
Calculation curvature around y and z axis caused by shrinkage
(1/ry) = -ecs(t,ts)·CoefReinf·å(Esi·Asi·(tiz-zsi))/(Eceff·Iiy)
(1/rz) = -ecs(t,ts)·CoefReinf·å(Esi·Asi·(tiy-ysi))/(Eceff·Iiz)
where
-ecs(t,ts)· - is total shrinkage strain, see "Parameters for calculation of shrinkage strain"
Coefreinf is coefficient increasing amount of reinforcement, see "Coefficient for increasing amount of reinforcement"
Esi - is modulus of elesticity of i-th bar of reinforcement
Asi - is area of reinforcement of i-th bar of reinforcement
ysi – position of i-th bar of reinforcement from centre of gravity of cross-section in y-direction
zsi – position of i-th bar of reinforcement from centre of gravity of cross-section in z-direction
tiy – distance between centre of gravity transformed uncracked/cracked cross-section and centre of gravity of concrete cross-section in y-direction
tiz – distance between centre of gravity transformed uncracked/cracked cross-section and centre of gravity of concrete cross-section in z-direction
Eceff - is effective module elasticity of the concrete calculated according formula Ec = Ec,eff = Ecm/(1+j).
Ecm -secant modulus of elasticity of concrete
j is creep coefficient, see "Parameters for calculation of creep coefficient "
Ai - transformed area uncracked/cracked cross-section
Iiy - transformed second moment of area around y-axis of uncracked/cracked cross-section calculated to centre of gravity transformed uncracked/cracked cross-section
Iiz - transformed second moment of area around z axis of uncracked/cracked cross-section calculated to centre of gravity transformed uncracked/cracked cross-section
Calculation stiffnesses for shrinkage
The stiffness of uncracked/cracked cross-section for shrinkage is calculated from strain and curvatures caused by shrinkage with using total level of load (total load combination)
-
bending stiffness around y-axis EIy =Mtot,y/(1/ry)
-
bending stiffness around z axis EIz = Mtot,z/(1/rz)
-
axial stiffness EA = Ntot/ex