Theoretical background

Calculation procedure

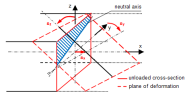
Imagine a diagram representing the strain in a reinforced concrete cross-section. Generally, the cross-section can be non-symmetric to y or z axis and loaded with a combination of N, M_y and M_z. Then the vector of strain consists of three non-zero values ε = {ε_x; ε_y, ε_z}. This vector determines so called plane of deformation (see following figure). More information can be found in VONDRÁČEK, R.: Numerical Methods in Nonlinear Concrete Design, Diploma thesis, 2000.

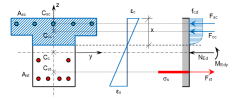
Corresponding plane of strain for plane of equilibrium in one plane bending only (M_y) is shown in following figure. Nevertheless, the distribution of the stress in compression part depends on type of stress-strain diagram of concrete. When bilinear diagram is used then distribution is constant or linear constant. In case of parabola-rectangular diagram the stress distribution is constant or linear-parabola.

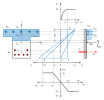
The previous figure shows a non specific case, but let us imagine an ultimate state. Under the ultimate state, we understand a case, where either concrete or steel is strained to limit value. We can draw some cases in a similar diagram. The basic assumptions of this limit strain method show the following figure. Generally, four limit strain states can occur. The numbering (1-4) in the following figure represents particular state types of the cross-section. The state (1) corresponds to the optimal failure when ultimate compressive strain in concrete (ε_cu) and ultimate tensile strain in reinforcement (ε_ud) are reached. In case of state (2), the ultimate limit strain in concrete is assumed within considering the strain in prestressing at the beginning of plastic branch (ε_s). The state (3) expresses the starting of the concrete crushing. Finally, the state (4) represents the reaching of ultimate compressive strain for axially loaded member decreased due to brittle failure effect.

The following checks are performed

• Check of compressive concrete

verification of strains: ε^cc / ε_cc,lim

verification of stresses: σ^cc / σ_cc,lim

• Check of compressive reinforcement

verification of strains: ε^sc / ε_sc,lim

verification of stresses: σ^sc / σ_sc,lim

• Check of tensile reinforcement

verification of strains: ε^st / ε_st,lim

verification of stresses: σ^st / σ_st,lim

Unity check is maximum from all partial unity checks. It means

UC = max(ε^cc / ε_cc,lim; σ^cc / σ_cc,lim; ε^sc / ε_sc,lim; σ^sc / σ_sc,lim; ε^st / ε_st,lim; σ^st / σ_st,lim)

where

εcc	the most compressive strain in concrete
εcc,lim	the limit of compressive strain in concrete
σcc	the most compressive stress in concrete
σsc,lim	the limit of compressive stress in concrete
εsc	the most compressive strain in reinforcement
εsc,lim	the limit of compressive strain in reinforcement
σsc	the most compressive stress in reinforcement
σsc,lim	the limit of compressive stress in reinforcement
εst	the most tensile strain in reinforcement
εst,lim	the limit of tensile strain in reinforcement
σst	the most tensile stress in reinforcement
σst,lim	the limit of tensile stress in reinforcement

Output values

There are presented the following output values:

• UC - unity check of check response (see above)
• ε_cc - maximal value of compressive strain of concrete
• ε_sc - maximal value of compressive strain of reinforcement
• ε_st - maximal value of tensile strain of reinforcement

• σ_cc - maximal value of compressive stress of concrete

• σ_sc - maximal value of compressive stress of reinforcement
• σ_st - maximal value of tensile stress of reinforcement
• x - depth of neutral axis in the direction perpendicular to neutral axis
• d - effective depth of cross-section in the direction perpendicular to neutral axis
• z - inner lever arm in the direction perpendicular to neutral axis