Comparison of PNL and PGNL calculation

The names PNL calculation (or analysis) (physically non-linear calculation) and PGNL calculation (or analysis) (physically and geometrically non-linear calculation) are taken from previous versions of the software. These terms are very similar and may be a bit misleading.

Therefore, it is useful to start with a few words about the features and principles of the two types of analysis.

First of all, it may be reasonable to establish more explanatory names.

$image\attention_16x16.gif$

What was known as a PNL calculation should be called:

calculation of deflections according to a standard.

IMPORTANT: Starting from version 2008.1 the term PNL was replaced by more suitable Code Dependent Deflections (CDD)

$image\attention_16x16.gif$

What was known as a PGNL calculation should be called:

physically (and geometrically) non-linear calculation.

$image\attention_16x16.gif$

It is not a rule that both types of non-linearity must be engaged in the latter, there are three possibilities:

(i) only physical non-linearity is taken into account,

(ii) only geometrical non-linearity is taken into account,

(iii) both physical non-linearity and geometrical non-linearity are taken into account.

This fact in turn may lead to shortening of the name of the second calculation type to "physically non-linear calculation" which may be abbreviated PNL. Now you can see one of the reasons why a more reasonable naming should be introduced.

The second reason is that the old PNL calculation (CDD from version 2008.1 on) is not a real physically non-linear calculation in terms of finite element method (contrary to PGNL that is a real non-linear calculation). It is a two-step solution following exactly the regulations given in technical standards for design and checking of concrete structures.

Both analyses are aimed primarily at concrete structures. The "calculation of deflections according to a standard" has been designed exclusively for concrete beams and plates, as it is based on the wording of technical standards for design and checking of concrete structures.

The "physically (and geometrically) non-linear calculation" is a general procedure tailored for the analysis of concrete frames (as it takes into account the provided reinforcement), but it is not limited to such structures.

Calculation of deflections according to standards

This calculation of deflections depends (is based) on standards. Therefore, it represents a standard-related calculation that is performed in two steps. First, a normal linear calculation is carried out and the computed internal forces are used to input the reinforcement (the provided reinforcement) or at least to determine the required reinforcement areas. The procedure continues with the calculation of cracks and their effect on the stiffness of individual elements. This weakening is then input into the solver. Finally, the calculation (linear one) is run once more with these reduced stiffnesses taken into account. Which is exactly what the technical standards require.

The short-term deflection is calculated. This deflection is multiplied by the creep coefficient φ and the long-term deflection is obtained. It is known that the elastic deflection multiplied by the creep coefficient φ equals to the deflection due to creep. Then, we add the long-term deflection to the short-term deflection and get the total deflection that can be assessed in accordance with the standards.

This calculation of the effects of creep is simplified and can be used for a limited set of situations. In fact, in case of reinforced concrete it covers most possible situations, as the history of assembly does not have to be followed. In other words, if the history of assembly steps does not have to be followed, this procedure can be applied.

The procedure is based on the method of effective modulus of elasticity E_f:

$image\effectivemodule.gif$

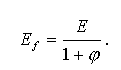
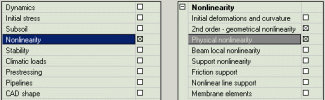
Physically (and geometrically) non-linear calculation

The Physically (and geometrically) non-linear calculation (i.e. what was so far called PGNL) is something completely different. It is a physically and/or geometrically non-linear calculation that can be applied to frame structures, contrary to Calculation of deflections according to a standards that can be used also for the analysis of plates. The Physically (and geometrically) non-linear calculation can be used for planar and spatial frame structures. If a plate (or generally a shell) is present in the analysed structure, such a model is analysed as well, but the plate (shell) is taken as a linear element. The same approach is applied if a steel (or other material) beam appears in the model of the structure.

For frame structures, we take into account the effect of cracks, plasticity and other factors on the stiffness. The problem is solved by means of a real non-linear calculation, i.e. using the iteration and secant method, i.e. the Newton-Raphson method that is implemented in SCIA Engineer. Fully physically and/or geometrically non-linear calculation is performed. It is necessary to select in the Functionality settings, which non-linearity is to be used: (i) physical, (ii) geometrical, or (iii) both. Through this setting the solver recognises what type of calculation should be started.

$image\PGNL_Functionality.gif$

We apply some load and find out that cracking occurs and determine the weakened cross-section (in fact, this is a bit more complicated, but the full description of the problem exceeds the scope of this text, for more details read [1]). The stiffness is modified in places where cracks appear and the calculation run once more. We calculate internal forces that are based on the modified stiffness, but the new internal forces usually still do not correspond to the stiffnesses. Therefore, we have to determine the stiffnesses once more. And this procedure is repeated as many times as necessary to meet the convergence criterion. The Physically (and geometrically) non-linear calculation is a calculation performed in several, usually many steps and the result is such a state of the structure when strain corresponds to internal forces (contrary to Calculation of deflections according to a standards calculation).

This is the way to find the limit resistance not of a single section, but of the whole structure. And it is the main goal of the Physically (and geometrically) non-linear calculation analysis.