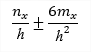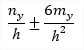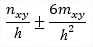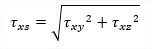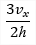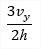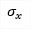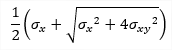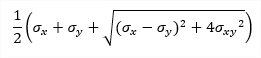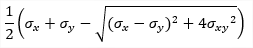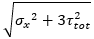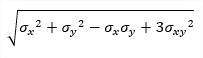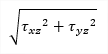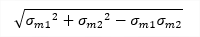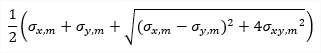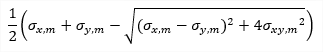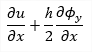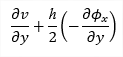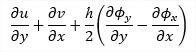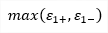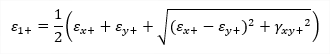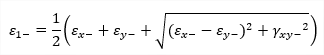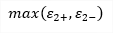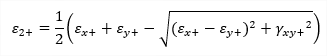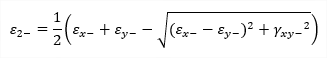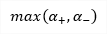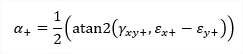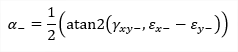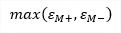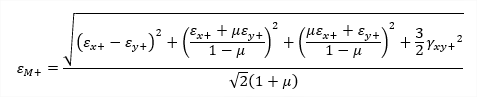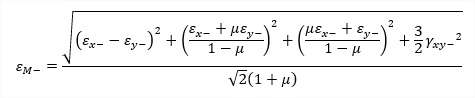3D stress / strain
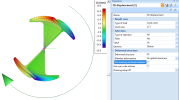
The 3D stress command serves for displaying stress and strain on selected 1D and 2D members. (not only results from linear and nonlinear analysis, but also stress and strain of modal and stability eigenmodes)
Usage
- Calculate a FEM analysis of the model
- Go to Tree > Results > 3D stress
- Set properties of the command to specify mainly:
- Click on [Refresh] action button to display the results
Note: To get general overview about how to work with Result service and its commands, see Results/Basics.
Properties
| Category | Property | Description / Notes |
|---|---|---|
| Selections |
Type of selection All / Current / Advanced / Named Selection / Design Group
|
Specifies on what members the results are displayed |
|
Filter No / Cross-section / Material / WildCard / Layer / Thickness / Type of beam |
Specifies the filter of members on what the results are displayed See "Filter" |
|
|
Location In nodes no avg. / In nodes avg. on macro |
Defines location in finite element mesh of calculated 2D values . |
|
| Trajectories
On/Off |
Available only for Principal magnitudes / Membrane magnitudes (2D) Displaying results of stresses by trajectories in direction of stress |
|
| Type variables
Basic magnitudes / Principal magnitudes / Membrane magnitudes (2D) / Basic total strain (2D) / Principal total strain (2D) / Basic plastic strain (2D) / Principal plastic strain (2D) |
||
| Value | See table Values below. | |
| Consider torsion due to shear centre eccentricity
On/Off |
With this option ON, the shear forces are considered to act in the centre of gravity and therefore the shear stresses are magnified by additional torsion effect from eccentricity of shear forces. Shear stresses on 1D members are calculated by default from shear forces and torsion moment, where shear forces are considered to act in the shear centre of the beam's cross-section. In case of cross-section with different position of shear centre with respect to the centroid of gravity this approach leads to discrepancy in the position of acting forces. Typical example of such cross-section is hot-rolled U shaped cross-section. |
|
| System
LCS mesh element / Global |
Defines in which coordinate system the results are displayed. |
|
| Extreme 1D
Fiber / Section / Cross-section / Design group / Member / Global |
Defines for which extreme on 1D member the results are displayed. |
|
| Extreme 2D
Mesh / Surface / Member / Global |
Defines for which extreme on 2D member the results are displayed. |
|
| Result case | Type of load
Load case / Combinations / Classes / Nonlinear Combinations/ Stability Combinations / Mass combinations |
Defines for what load the results are displayed.
|
| Envelope (for 2D drawing)
Minimum / Maximum / Absolute extreme |
||
| Calculate results on ... | 1D members
On / Off |
It is possible to switch ON/OFF drawing of results on 1D members or faces of 2D members. positive faceis the face which is on +z local coordinate of the 2D member negative face is on -z local coordinate of the 2D member |
| 2D positive face
On / Off |
||
| 2D negative face
On / Off |
||
| Deformed structure |
Deformed structure On / Off |
The result values can be displayed also on deformed surface of the structure The deformed surface is displayed for the combination from selected result case which provides the extreme value of selected magnitude. In case the result type contains envelope combination (different combinations can give extreme values for each member of the structure) it is possible to select between "Member deformation for global / local maximum". Note: Member deformation for global maximum means that the deformation of surfaces is calculated just for one exact combination which gives global extreme of selected magnitude. Member deformation for member maximum means that the extreme combination is evaluated for each member separately. In this case the deformed surface can be displayed for different combinations per each member and there can be discontinuities in deformed surface. |
| For drawing use linear rotation
On / Off |
Enables to switch between small displacement assumption based linear translations (which provides result consistent with used assumption) and circular translations (which keeps the original shape of cross section). Linear translation ON / OFF |
|
| Drawing Setup 2D | "Drawing setup 2D" | |
| Errors, warnings and notes settings | "Errors, warnings and notes settings" |
Values
The following categories of stresses and strains can be displayed:
Note: As default, the stresses and strains refer to the local axes of the individual finite (mesh) elements. The local axes can be displayed by selecting the corresponding option in the View parameters settings.
Basic magnitudes
The basic stresses are default magnitudes referring to the local axes of the selected coordination system.
| Value | Description | Notes |
|---|---|---|
| σx(1D/2D) |
stress in direction of local axis x |
It is calculated on assumption of linear distribution of the strain within the section. In the first step the plane of deformation is calculated using iterative algorithm () so strain in all fibres is known. In the next step adequate stresses are assigned using stress-strain curve. Remember that linear calculation uses linear approximation (E modulus) of stress-strain curve. |
| σy(2D) |
stress in direction of local axis y |
|
| txy(2D) |
shear stress |
The shear stresses are evaluated differently for thick-walled and thin-walled cross section. For thick-walled (solid) sections the real txyor txzare calculated and displayed. For thin-walled sections the final shear flow from unit forces in Y or Z directions are evaluated and displayed as total shear flow: See also chapters in manual related to calculation of sectional characteristics.
|
| txz(2D) |
shear stress perpendicular to the plane |
|
| tyz(2D) |
shear stress perpendicular to the plane |
|
| txy/txs(1D) | shear stresses in local coordinates (thick walled cross sections) or total shear flow (thin walled cross sections) |
They are calculated from the shear force and torsional moment using unit distribution of shear stresses. Those unit distributions of shear stresses are also available in the cross section editing dialogue. The txs magnitude represents: the total shear flow which is in the thin-walled cross section. Distribution of this shear flow from horizontal a vertical unit shear forces can be checked in the cross section manager. |
| txz/txs(1D) |
Principal magnitudes
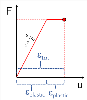
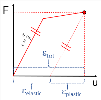
The principal stresses represent the extreme values of the internal forces derived from the basic ones by transformation into the directions of principal axes:
| Value | Description | Notes |
|---|---|---|
| σ1 |
principal stress 1D - consider torsion due shear force is OFF: 1D - consider torsion due shear force is ON: 2D:
|
1) The angles of principal magnitudes are derived from to the local axis x. 2)The principal magnitudes can be visualized also as trajectories (see the option Trajectories in the command properties). |
| σ2 |
principal stress |
|
| σE |
equivalent stress (von Mises) 1D: 2D: |
|
| tmax,b(2D) |
Maximum shear stress perpendicular to the plane
|
Membrane magnitudes (2D)
| Value | Description | Notes |
|---|---|---|
| σmE |
|
|
| σm1 |
principal membrane stress on positive face (max) |
|
| σm2 |
principal membrane stress on positive face (min) |
Basic total strain (2D)
The basic strains are default magnitudes referring to the local axes of the selected coordination system.
| Value | Description | Notes |
|---|---|---|
| etot,x |
strain on positive surface |
|
| etot,y |
strain on positive surface |
|
| gtot,xy |
slope on positive surface |
Principal total strain (2D)
The principal strains represent the extreme values of the internal forces derived from the basic ones by transformation into the directions of principal axes:
| Value | Description | Notes |
|---|---|---|
| etot,1 |
maximum principal strain |
principal strain on positive surface (max) principal strain on negative surface (max)
|
| etot,2 |
maximum principal strain |
principal strain on positive surface (min) principal strain on negative surface (min) |
| a |
maximum angle of principal strain |
angle of principal strain on positive surface angle of principal strain on negative surface |
| etot,M |
maximum equivalent strain (Mises) |
equivalent strain on positive surface (Mises) equivalent strain on negative surface (Mises) |
Basic plastic strain (2D)
The basic plastic strains are default magnitudes referring to the local axes of the selected coordination system. The basic plastic strains are part of basic total strains after nonlinear calculation with functionality "General plasticity" for elasto-plastic material.
| Value | Description | |
|---|---|---|
| epl,x |
for elasto-plastic material without hardering for elasto-plastic material with hardering |
|
| epl,y | ||
| gpl,xy | ||
Principal plastic strain (2D)
The principal plastic strains represent the extreme values of the internal forces derived from the basic ones by transformation into the directions of principal axes. The principal plastic strains are part of principal total strains after nonlinear calculation with functionality "General plasticity" for elasto-plastic material.
| Value | Description | |
|---|---|---|
| epl,1 |
for elasto-plastic material without hardering for elasto-plastic material with hardering |
|
| epl,2 | ||
| a | ||
| epl,M | ||
Limitations
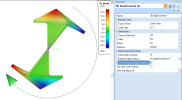
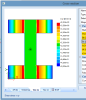
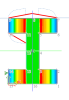
It is necessary to take into account that result are calculated in fibres only. Values between fibres are linearly interpolated. In some cases this precondition results in omitting of some local extremes. Example of this phenomenon is visible on following pictures:
There is a thick-walled I cross section exposed to horizontal shear force:
The third picture shows distribution of shear XY on the edge between fibres 7, 9. The theoretical distribution is shown by the dashed light blue line. the red line shows distribution which is presented by the 3D stress result. The reason is quite clear. The distribution of stresses is linear interpolation between values in fibres and the only fibre between fibres 7 and 9 is fibre 8 which has quite low value. Therefore the higher shear stress on exceeding parts of flanges are not respected on this edge.
This higher shear stress from exceeding part of flanges is displayed correctly on the inner edge 10-11 as is also visible on the picture.