Calculation buckling ratio – general formula
For the calculation of the buckling ratios, some approximate formulas are used. These formulas are treated in reference [1], [2] and [3].
The following formulas are used for the buckling ratios (Ref[1],pp.21) :
- for a non sway structure :

- for a sway structure :

with:
|
L |
the system length |
|
E |
the modulus of Young |
|
I |
the moment of inertia |
|
Ci |
|
|
Mi |
the moment in node i |
|
Fi |
the rotation in node i |
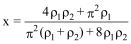
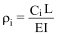

The values for Mi and φi are approximately determined by the internal forces and the deformations, calculated by load cases which generate deformation forms, having an affinity with the buckling form. (See also Ref.[5], pp.113 and Ref.[6],pp.112).
The following load cases are considered:
- load case 1 : on the beams, the local distributed loads qy=1 N/m and qz=-100 N/m are used, on the columns the global distributed loads Qx = 10000 N/m and Qy =10000 N/m are used.
- load case 2 : on the beams, the local distributed loads qy=-1 N/m and qz=-100 N/m are used, on the columns the global distributed loads Qx = -10000 N/m and Qy= -10000 N/m are used.
In addition, the following limitations apply (Ref[1],pp.21):
- The values of ρi are limited to a minimum of 0.0001
- The values of ρi are limited to a maximum of 1000
- The indices are determined such that ρ1 ≥ ρ2
- Specifically for the non-sway case, if ρ1 ≥ 1000 and ρ2 ≤ 0,34 the ratio l/L is set to 0,7
The used approach gives good results for frame structures with perpendicular rigid or semi-rigid beam connections. For other cases, the user has to evaluate the presented bucking ratios. In such cases a more refined approach (from stability analysis) can be applied.
