Primary effects

Basics

The primary effects of a load are the effects (internal forces, deformations) of that load on the 1D finite element where it is applied, without considering any connection to the rest of the structure or, more precisely, considering that every single mesh node of the structure is supported with a fixed support.

In essence, primary effects describe what is happening inside a 1D element, between its nodes. Without primary effects, all results in a 1D element could only be linearly interpolated between the nodal values, leading to a very poor readability of the results.

In the normal case, primary effects are simply taken into account in the background, without any particular intervention of the user. However, SCIA Engineer allows to display them separately.

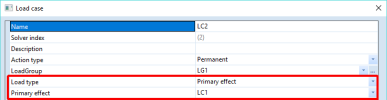
In SCIA Engineer, the primary effects of some static load case LC1 can be accessed by creating a new load case, LC2, and defining it as the primary effects of load case LC1. See also the chapter related to load cases.

Example 1: simply supported beam

Consider the following example:

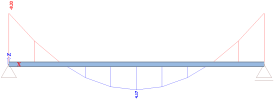
A 10m long simply supported beam; in load case LC1, a uniform load q = 1 kN/m is applied.

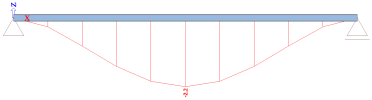
A second load case, LC2, is defined as the primary effects of LC1:

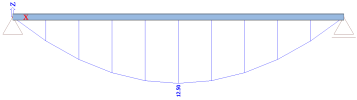
The results for LC1 are, for the bending moment, corresponding to a simply supported beam:

And for the deflection:

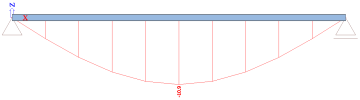
For load case LC2, the results correspond to a beam with both ends fixed:

Still considering the same example, but refining the mesh, setting the average number of tiles of 1D members to 2 (instead of 1), the results of LC2 will be as if there would be an additional fixed support in the middle of the beam. The beam is now analyzed with two finite elements.

Purpose of primary effects

In essence, the finite element analysis computes results only in selected points. Which points are relevant depend on the type of formulation of the finite elements that are used. In SCIA Engineer 1D finite elements, both displacements and internal forces are primarily computed at the mesh nodes - and only there.

The purpose of primary effects is to obtain accurate results inside each beam element, between the mesh nodes. The primary effects are calculated analytically and take into account, for instance, local effects due to an irregular distribution of the applied loads. After finite element resolution, they are used to interpolate between nodal results, in order to obtain results along the entire 1D elements.

That approach allows for accurate results along the entire beam, without further refining the mesh.

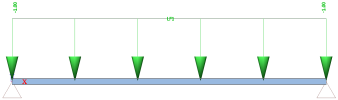
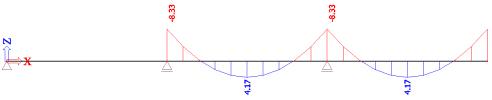
Example 2: continuous beam

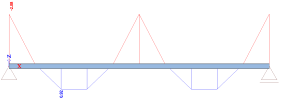
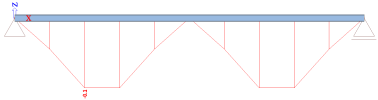
Bending moment My

Nodal results

Primary effects

Shear force Vz

Nodal results

Primary effects

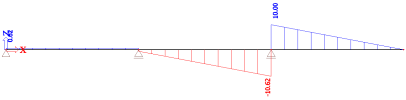
Normal force N

Nodal results

Primary effects

Please note here, that there is no primary effect, because the axial load is applied directly to a node, hence there is no local effect inside any of the 1D elements. The final distribution of N comes entirely from the nodal results.

Deflection uz

Nodal results

Primary effects