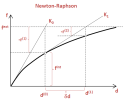
Newton-Raphson method

It is a tangent method which calculate in every step stiffness matrix of structure, but convergence is mostly in several iterations. This method is robust for most of problems. It may, however, fail in the vicinity of inflection points of loading diagram. It provides for solution of extremely large deformations. The accuracy of the method can be increased through refinement of the finite element mesh or by the increase in total number of increments. For example, the solution of a single beam divided to a single finite element will not give sufficient results. This method requires that a 1D member is divided to at least four (4) finite elements.

The rotation achieved in one increment should not exceed 5°.

In some specific cases, high number of increments may solve even problems that tend to a singular solution which is typical for the analysis of post-critical states.

Note : This method requires that a 1D member is divided to at least four (4) finite elements. Usually, such division is adjusted automatically whenever Newton-Raphson method is selected for calculation.