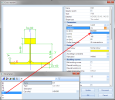
Available parameter types

There are numerous parameters types available in SCIA Engineer. Each type may be used for other model entity, some are intended for geometry, others for loads, others for cross-sections, etc.

Parameter types

Nothing	The parameter is not used.
Integer	The parameter is used as an integer.
Coefficient	The parameter is used as coefficient.
Length	The parameter is used for definition of length in the model.
Force	The parameter is used for definition of size of force load.
Moment	The parameter is used for definition of size of moment load.
Line load	The parameter is used for definition of size of line load.
Surface load	The parameter is used for definition of size of surface load.
Mass	The parameter is used for definition of size of masses.
Line mass	The parameter is used for definition of size of line masses.
Surface mass	The parameter is used for definition of size of surface masses.
Cross-section length	The parameter is used for definition of length at cross-sections.
Angle	The parameter is used for definition of angles.
Relative	The parameter is used for definition of relative values.
Boolean	This parameter can have two values only: True (ON) or False (OFF).
Time (history)	Time of individual construction stages on time-line.
Library	This parameter type can be used with any "library" item, i.e. any item that is selected from one of SCIA Engineer’s internal databases, such as materials, cross-sections, subsoil, reinforcement pattern, etc. The Value represents the parametrized item and the Alternative represents the value which will be used in the parametrized item. remark: The selector switch in the parametrized item must be checked in the Material library.
Combination factor	Combination factors for load cases inserted into a combination.
Relative humidity	Applicable in the calculation of long term losses in prestress.
Stress	(i) Stress in concrete that can be defined in measured values when the Time Dependant Analysis is performed or (ii) the initial stress of the strands for a strand pattern.
Temperature	Used for temperature.
Length for stiffness	Used to define length unit in stiffness.
Point stiffness	Used to define point stiffness.
Line stiffness	Used to define line stiffness.
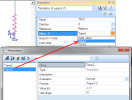
Reinforcement diameter	Used to define the diameter of reinforcement bars.
Translation	Used to define the support translation Value - U in the Point displacement load.
Rotation	Used to define the support rotation Value - R in the Point displacement load.
Reverse parameters	It allows to define a parameter which loads some value from cross section or structure node. This parameter maybe used in another parameter as value or in the formula.
Area	Used in the parameter set for templates and this then link with a formula to calculate some different value.
Reinforcement area	Used for the editing of the transverse bending reinforcement area. See the chapter Edit distance of transverse bending reinforcement in the topic Design of transverse reinforcement in flange of cross-section according to EN 1992-1-1.
List	Allows user to create a list of parameters Exposure class and fire duration. This list is used for Hollow core slab.
Slab bending stiffness	Used to define slab bending stiffness. It can be used for the plate orthotropy definition.
Reinforcement diameter number	Used in IBC code for the parametrization of the reinforcement diameter when the size number is used.
Cross-section rolled	The parameter is used for definition of rolled cross-sections.

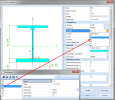
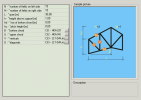
Example

The following Template dialogue contains parameters of several types:

$image\templatedialogue.gif$

M, N	integer
L, h, hd, hu	length
B, U, V, D	library

Value types

Value	A specific numerical value is defined directly.
Formula	The value of the parameter is given in the form of a simple formula..

Formula

Formula may consist of several values, parameters, functions and operators. Putting individual members of the expression into brackets "()" may change the priority of evaluation. Available operators and functions are:

Addition

Symbol: "+"

Example: a+b

Subtraction

Symbol: "-"

Example: a-b

Multiplication

Symbol: "*"

Example: a*b

Modulo

Symbol: "\"

The modulo operation finds the remainder of division of one number by another.

Given two numbers, a (the dividend) and n (the divisor), a modulo n (abbreviated as a mod n) is the remainder, on division of a by n. For instance, the expression "7 mod 3" would evaluate to 1, while "9 mod 3" would evaluate to 0. (source: http://en.wikipedia.org)

Example: a\b

Note: see Units

Division

Symbol: "/"

Example: a/b

Power / Exponentiation

Symbol: "^"

Exponentiation is a mathematical operation, written an, involving two numbers, the base a and the exponent n. When n is a positive integer, exponentiation corresponds to repeated multiplication. (source: http://en.wikipedia.org)

Example: a^b

Lower than

Symbol: "<"

Example: (a<b)*2+5

This reads:

If a is lower than b, the result is TRUE (=1). Thus we get formula 1*2+5=7.

If a is not lower than b, the result is FALSE (=0). Thus we get formula 0*2+5=5.

Lower than or equal

Symbol: "<="

Example: (a<=b)*2+5

Equal to

Symbol: "=="

Example: (a==b)*2+5

Not equal to

Symbol: "<>"

Example: (a<>b)*2+5

Greater than or equal

Symbol: ">="

Example: (a>=b)*2+5

Greater than

Symbol: ">"

Example: (a>b)*2+5

Absolute value

Symbol: "abs"

Example: abs(a)

Maximum

Symbol: "max"

Example: max(a;b;c;d)

Minimum

Symbol: "min"

Example: min(a;b;c;d)

Average

Symbol: "average"

This function calculates the average value of the specified parameters.

Example: average(a;b;c;d)

Sine

Symbol: "sin"

Example: sin(a)

Cosine

Symbol: "cos"

Example: cos(a)

Tangent

Symbol: "tan" or "tg"

Example: tan(a) or tg(a)

Arcsine

Symbol: "arcsin" or "asin"

Example: arcsin(a) or asin(a)

Arccosine

Symbol: "arccos" or "acos"

Example: arccos(a) or acos(a)

Arctangent

Symbol: "arctan" or "atan" or "arctg"

Example: arctan(a) or atan(a) or arcctg(a)

Natural logarithm

Symbol: "ln"

The natural logarithm, formerly known as the hyperbolic logarithm, is the logarithm to the base e, where e is an irrational constant approximately equal to 2.718281828459. In simple terms, the natural logarithm of a number x is the power to which e would have to be raised to equal x — for example the natural log of e itself is 1 because e1 = e, while the natural logarithm of 1 would be 0, since e0 = 1. The natural logarithm can be defined for all positive real numbers x as the area under the curve y = 1/t from 1 to x, and can also be defined for non-zero complex numbers as explained below. (source: http://en.wikipedia.org)

Example: ln(a)

Common logarithm (decadic logarithm)

Symbol: "log"

In mathematics, the common logarithm is the logarithm with base 10. It is also known as the decadic logarithm, named after its base. (source: http://en.wikipedia.org)

Example: log(a)

Exponential function

Symbol: "exp"

The exponential function is one of the most important functions in mathematics. The application of this function to a value x is written as exp(x). Equivalently, this can be written in the form ex, where e is a mathematical constant, the base of the natural logarithm, which equals approximately 2.718281828, and is also known as Euler's number. (source: http://en.wikipedia.org)

Example: exp(a)

Sign

Symbol: "sign" or "sgn"

The function returns "1" for positive numbers, "-1" for negative numbers, and "0" for zero.

Example: sign(a) or sgn(a)

Square root

Symbol: "sqrt"

Example: sqrt(a)

Integer

Symbol: "int"

This operation is truncation or the round to zero method, a mixture of the floor and ceiling function: for positive or 0 x it returns floor(x), and for negative x it returns ceiling(x). (source: http://en.wikipedia.org)

Example: int(a)

Note: see Units

Floor

Symbol: "floor"

The floor function of a real number x, denoted floor(x), is a function that returns the highest integer less than or equal to x. (source: http://en.wikipedia.org)

Example: floor(a)

Note: see Units

Ceiling

Symbol: "ceil"

The ceiling function, denoted ceil(x), is the function that returns the smallest integer not less than x. (source: http://en.wikipedia.org)

Example: ceil(a)

Note: see Units

Fractional part

Symbol: "frac"

This operation returns the fractional part of a real number, i.e. the digits located after the comma. For instance frac(12.345) = 0.345.

Example: frac(a)

Note: see Units

Conjunction, AND

Symbol: "&&"

Logical conjunction or and is a two-place logical operation that results in a value of true if both of its operands are true, otherwise a value of false. (source: http://en.wikipedia.org)

Example: a&&b

Disjunction, OR

Symbol: "||"

Logical disjunction or inclusive disjunction is a logical operator that results in true whenever one or more of its operands are true. (source: http://en.wikipedia.org)

Example: a||b

Exclusive disjunction, XOR

Symbol: "^^"

The logical operation exclusive disjunction, also called exclusive or, (symbolized XOR or EOR), is a type of logical disjunction on two operands that results in a value of "true" if and only if exactly one of the operands has a value of "true". (source: http://en.wikipedia.org)

Example: a^^b

Not

Symbol: "not"

The function returns the opposite logical value (true / false) of the parameter.

Example: not(a)

Examples

formula	result
3*5+5	20
3*(5+5)	30
sin(90)	1
10*cos(45)	7.07
3^3	27
log(10)	1
ln(2.718281828)	1

Use range

It is possible to define the range in which each of the input parameters is valid. Thus one can verify the input values that are inserted when later the template is opened.

Units

All values are stored in SI units. Consequently:

Constants used in formulas are always in SI units. If you want to have it in units defined in the Units setup, you cannot use constants in formula. Prefer using pre-declared parameters of type Value.

Functions and operators are always applied to values in SI units. Some functions and operators work with the integer or fraction part of their argument (modulo, int, floor, ceil, frac). Following said rule, they are applied to the SI value of their argument. For instance, if a = 12.3456 kN, int(a) returns 12.3450, because a = 12345.6 N in SI units.