Combined Shear Force, Axial Force and Bending Moment

The Combined Shear Force, Axial Force and Bending Moment Check is executed according to EN 1993-1-3 art. 6.1.10.

In the following paragraphs formula (6.27) is written out for both directions.

Shear Vy

In case of shear Vy formula (6.27) is written out as follows:

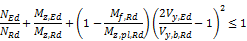
Remarks:

• M_f,Rd is taken as zero in case of Vy

(In case of weak axis bending, the ‘web’ becomes a ‘flange’. Since there is only a single ‘flange’ in that case, the moment resistance of this flange is negligible. In addition, in case of more webs like in a box section EN 1993-1-5 art. 7.1 (5) specifies M_f,Rd = 0. Therefore, as a general conservative approach for Vy the value of M_f,Rd is taken as 0.)

Shear Vz

In case of shear Vz formula (6.27) is written out as follows:

Remarks:

• According to [Ref.16] pp70  M_f,Rd is calculated as follows:

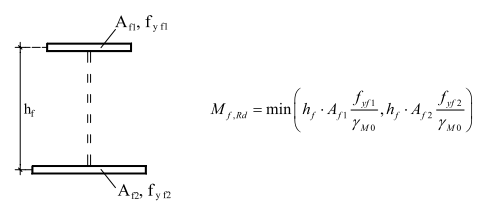
This is generalised in the following way:

1. Only elements with element types I, UO and SO are accounted for
2. Only elements which have an angle α with the principal y-y axis which is ≤ 45° are considered
   
   In case there is only one or none of such element, M_f,Rd = 0.
3. Of these elements, the one with the lowest b_eff is considered. The width b_eff concerns the effective with of this element, read from the effective shape for bending.
4. A_f = b_eff * t with t the thickness of the considered element.
   
5. Next only elements which have an angle α with the principal y-y axis which is > 45°are considered.
   
   In case there are no such elements, set M_f,Rd = 0.
6. Of these elements, the one with the highest value of l_c * sin(α) is considered, with l_c the centreline length of the element.
7. h_f = l_c * sin(α)
8. M_f,Rd is now be calculated as:
   

 

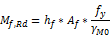
• According to [Ref.16] pp70  M_pl,Rd is calculated as follows:

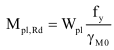
with W_pl read from the gross section properties.