General plasticity
A general plastic analysis can be carried out in SCIA Engineer for any 2D members (plates, walls, shells).
There are four types of general plasticity in Scia Engineer : Tresca, von Mises, Drucker-Prager and Mohr-Coulomb.
The plastic behaviour of materials may be combined with other types of non-linearity in SCIA Engineer. For instance, plasticity, press only supports and large displacement analysis can be used together. Tension only 1D members with a plastic limit forces may be used to model the behaviour of bolts in a connection.
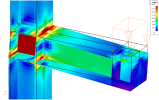
The typical first application of general plasticity is the detailed analysis of non-standard steel construction connections, where simplified methods do not apply. It may however be applied to any structure that can be modelled using 2D members.
Plasticity is not supported yet for 1D members. Any beam or truss member that is present in the model will be considered as elastic.
Theoretical background
Tresca yield criterion
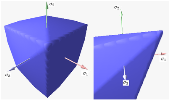
The Tresca yield criterion is taken to be the work of Henri Tresca. It is also known as the maximum shear stress theory (MSST) and the Tresca–Guest (TG) criterion. In terms of the principal stresses the Tresca criterion is expressed as:
Where is the yield strength in shear, and
is the tensile yield strength.
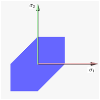
On the first picture there is the Tresca–Guest yield surface in the three-dimensional space of principal stresses. It is a prism of six sides and having infinite length. This means that the material remains elastic when all three principal stresses are roughly equivalent (a hydrostatic pressure), no matter how much it is compressed or stretched. However, when one of the principal stresses becomes smaller (or larger) than the others the material is subject to shearing. In such situations, if the shear stress reaches the yield limit then the material enters the plastic domain.
On the second picture there is the Tresca–Guest yield surface in two-dimensional stress space, it is a cross section of the prism along the plane.
source: Wikipedia http://en.wikipedia.org/wiki/Yield_surface#Tresca_yield_surface
Von Mises yield criterion
The von Mises yield criterion suggests that the yielding of materials begins when the second deviatoric stress invariant J2 reaches a critical value. For this reason, it is sometimes called the J2-plasticity or J2 flow theory. It is part of a plasticity theory that applies best to ductile materials, such as metals. Prior to yield, material response is assumed to be elastic.
In materials science and engineering the von Mises yield criterion can be also formulated in terms of the von Mises stress or equivalent tensile stress, , a scalar stress value that can be computed from the Cauchy stress tensor. In this case, a material is said to start yielding when its von Mises stress reaches a critical value known as the yield strength,
. The von Mises stress is used to predict yielding of materials under any loading condition from results of simple uniaxial tensile tests. The von Mises stress satisfies the property that two stress states with equal distortion energy have equal von Mises stress.
Because the von Mises yield criterion is independent of the first stress invariant, I1, it is applicable for the analysis of plastic deformation for ductile materials such as metals, as the onset of yield for these materials does not depend on the hydrostatic component of the stress tensor.
Although formulated by Maxwell in 1865, it is generally attributed to Richard Edler von Mises (1913). Tytus Maksymilian Huber (1904), in a paper in Polish, anticipated to some extent this criterion. This criterion is also referred to as the Maxwell–Huber–Hencky–von Mises theory.
The formulation of the von Mises comparison stress in a general 3D stress-state is given by:
source: Wikipedia http://en.wikipedia.org/wiki/Von_Mises_yield_criterion
Drucker-Prager yield criterion
The Drucker-Prager yield criterion is similar to the von Mises yield criterion, with provisions for handling materials with differing tensile and compressive yield strengths. This criterion is most often used for concrete where both normal and shear stresses can determine failure. The Drucker–Prager yield criterion may be expressed as
where
where
and
are the uniaxial yield stresses in compression and tension respectively. The formula reduces to the von Mises equation if
.
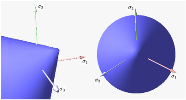
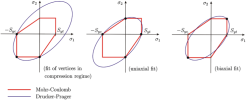
On the first picture there is Drucker–Prager yield surface in the three-dimensional space of principal stresses. It is a regular cone.
On the second picture there is Drucker–Prager yield surface in two-dimensional space. The elliptical elastic domain is a cross section of the cone on the plane of ;
.
It can be chosen to intersect the Mohr–Coulomb yield surface in different number of vertices. One choice is to intersect the Mohr–Coulomb yield surface at three vertices on either side of the line, but usually selected by convention to be those in the compression regime. Another choice is to intersect the Mohr–Coulomb yield surface at four vertices on both axes (uniaxial fit) or at two vertices on the diagonal
(biaxial fit).The Drucker-Prager yield criterion is also commonly expressed in terms of the material cohesion and friction angle.
source: Wikipedia http://en.wikipedia.org/wiki/Yield_surface#Drucker.E2.80.93Prager_yield_surface
Mohr-Coulomb yield criterion
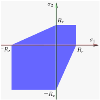
The Mohr-Coulomb yield is similar to the Tresca criterion, with additional provisions for materials with different tensile and compressive yield strengths. This model is often used to model concrete, soil or granular materials. The Mohr–Coulomb yield criterion may be expressed as:
Where
;
and the parameters and
are the yield (failure) stresses of the material in uniaxial compression and tension, respectively. The formula reduces to the Tresca criterion if
.
On the first picture there is Mohr–Coulomb yield surface in the three-dimensional space of principal stresses. It is a conical prism and determines the inclination angle of conical surface.
On the second picture there is Mohr–Coulomb yield surface in two-dimensional stress space. It is a cross section of this conical prism on the plane of ,
.
source: Wikipedia http://en.wikipedia.org/wiki/Yield_surface#Mohr.E2.80.93Coulomb_yield_surface
Finite element model
Drilling rotations at each node is used for in-plane loading. This means that element has six degrees of freedom at each node and is therefore compatible with other types of elements (beam/solid elements). Within the element area the Gauss 2x2 quadrature points are used. Each of these Gauss quadrature points is realized by nine Gauss-Lobatto quadrature points throughout the thickness, so the four-node element has 2x2x9=36 quadrature points in total. Due to these Gauss-Lobatto points the element can handle bending loading with high accuracy. In all of these points the nonlinear model is computed independently using the plane stress formulation. Linear transversal shear stiffness is assumed.
About Gauss-Lobatto quadrature: https://en.wikipedia.org/?title=Gaussian_quadrature
Using general plasticity in SCIA Engineer
General plasticity is a specific type of non-linearity in SCIA Engineer. After defining the suitable data in the project a non-linear analysis must be carried out to calculate the plastic behaviour of the structure. Please refer to the general information about non-linear analysis in SCIA Engineer.
Project settings
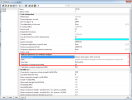
General plasticity is a sub-functionality of non-linear analysis. In the project settings, in the Functionality tab, enable Non-linearity and General plasticity.
Nonlinear properties of materials
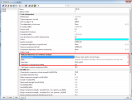
The non-linearity of materials is defined directly in the material library. See the property group Material behaviour for non-linear analysis. By default, all materials in the library are set as elastic. This means, that the selected material will behave elastically during a non-linear analysis. The plastic properties of materials are generic, code independent in SCIA Engineer and are therefore available for any material, regardless of the selected design code.
Plasticity can be enabled by selecting a type of plastic behaviour.
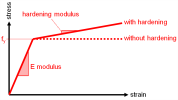
The stress-strain relationship is automatically generated from 3 parameters: Young's modulus (elastic part), yield stress for uniaxial tension and, optionally, hardening modulus (slope of the plastic branch).
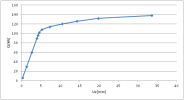
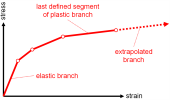
Only the tension part of the diagram is defined, as it is related to a plastification condition in general 3D stress state in principal stress directions. Some plastification models allow for a different yield stress in compression, which is defined separately. There is no limit (ultimate) strain value for the analysis. When the actual strain value in the structure exceeds the defined diagram, the diagram is extrapolated, tangent to the last defined segment of the stress-strain relationship. The reason for that is, that the analysis would then fail and it would be impossible for the user to find where the problem is located in the structure. It is therefore preferable, that the analysis continues and that the user checks the obtain strain values after the analysis.
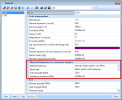
The following properties define the nonlinear behaviour of the material in the material library.
| E modulus | Young's modulus of the material; it defines the slope of the elastic part of the stress-strain relationship |
| Material behaviour |
selects the type of behaviour of the material in case of nonlinear analysis. The available types are currently:
|
| Input type |
type of definition of the plastic branch of the stress-strain relationship. The available types are:
|
| Yield |
elastic limit for plastification due to |
| Yield stress in uniaxial compression [MPa] | elastic limit for plastification due to compression |
| Hardening modulus | slope of the plastic branch of the stress-strain relationship |
Important: default values have been defined for the yield strength and the hardening modulus, as much as possible according to the corresponding design code of each material proposed in the system libraries. However, those values should always be reviewed before use.
Assigning plastic behaviour to a 2D member
To enable plastic behaviour on a 2D member, just assign to it a material whose plastic behaviour has been enabled. There is no other specific setting.
Although various types of non-linearity may be combined in the same project, it is not possible to cumulate several types of non-linearity on the same 2D member. The property FEM non-linear model, when combined with a plastic material, will behave as follows:
- Plastic material and 2D press-only behaviour: the press-only behaviour will be ignored and the 2D member will behave as plastic
- Plastic material and membrane behaviour: the plastic behaviour will be ignored and the 2D member will behave as an elastic membrane
Additionally, a warning message will be displayed when starting the analysis, giving the same information about functionality conflicts.
Using a non-linear material in the properties of the cross-section of a 1D member will not affect the behaviour of that member. General plasticity is currently not supported for 1D members and the behaviour of the material will remain elastic for such member.