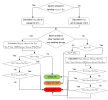
Calculation procedure

As mentioned above, it exists general concept of "strut-and-tie" model for the prediction of shear effects in concrete. In this model, the top compression and bottom tensile members represent the compressive concrete and tensile reinforcement, respectively. The horizontal members are connected by the compressive virtual struts and reinforcement tensile ties. The axial forces in tensile ties should be transmitted by the shear reinforcement. Consequently, the maximal force in concrete struts (V_Rd,max) and shear force retained by the shear resistance (V_Rd,s) have to be compared with acting shear force (V_Ed). The procedure for check can be represented by diagram below:

The formulas which are used for the calculation of each component of this model are the following.

Generally, there are two possibilities for calculation of shear capacity of concrete dependently on existence of cracks in bending:

Shear concrete capacity in region cracked in bending - formula 6.2.a,b in EN 1992-1-1

V_Rd,c = [C_Rd,c ∙ k ∙ (100 ∙ ρ_l ∙ f_ck)^1/3 + k₁ ∙ σ_cp] ∙ b_w ∙ d

V_Rd,c,min = (ν_min + k₁ ∙ σ_cp) ∙ b_w ∙ d

Shear concrete capacity in region uncracked in bending – clause 12.6.3(3) in EN 1992-1-1

V_Rd,c = f_cvd ∙ A_cc / k_12.6.3

Additionally, there is calculated maximal shear force (V_Ed,max)) without reduction by β for member where load is applied in the upper side of the member (see formula 6.5 in EN 1992-1-1).

V_Ed,max = 0,5 ∙ b_w1 ∙ d ∙ ν ∙ f_cd

Maximal capacity of concrete compressive strut (V_Rd,max) is determined according to formula 6.9 in EN 1992-1-1, because as has been mentioned before, the angle of stirrups (θ) is always perpendicular to member axis.

V_Rd,max = (α_cw ∙ b_w1 ∙ z ∙ ν₁ ∙f_cd) / (cot θ + tan θ)

Design value of shear force sustained by shear reinforcement (V_Rd,s) is calculated according to formula 6.13 in EN 1992-1-1

V_Rd,s = A_sw / s ∙ z ∙ f_ywd ∙ (cot θ + cot α) ∙ sin α

A_sw for formula 6.13 is limited to A_sw,max according clause 6.2.2(3)

A_sw,max = α_cw ∙ ν₁ ∙ b_w ∙ f_cd ∙ s_l / (f_ywd ∙ (1 + cotg(θ)²) ∙ sin α)

where

α_cw	Coefficient taking account of the state of the stress in the compression chord
ν₁	Strength reduction factor for concrete cracked in shear
b_w	Minimum width of cross-section in the tensile area
f_cd	Design concrete strength
f_ywd	Design yield strength of the shear reinforcement
s_l	Centre-to-centre distance of stirrups in longitudinal direction

Final design value of shear force (V_Rd) carried by member is calculated based on the following formulas depending on type of member and area of shear reinforcement.

for beam as slab and for other member with only detailing stirrups (A_sw = 0)

V_Rd = V_Rd,c ≤ min(V_Rd,max, V_Ed,max) + V_td + V_ccd

for other cases

V_Rd = V_Rd,s + V_td + V_ccd ≤ min(V_Rd,max, V_Ed,max) + V_td + V_ccd

where

V_Ed	resultant of shear force V_Ed = √(V_Ed,y² + V^Ed,z²)
V_Ed,y(z)	shear force in direction of y(z) axis of LCS
V_Rd,c	the design shear resistance of the member without shear reinforcement
σ_ct,max	maximal tensile strength in uncracked cross-section
V_Rd,c,min	the minimal value of design shear resistance of the member without shear reinforcement
C_Rd,c	coefficient for calculation V_Rd,c loaded from Manager for National annexes
k	coefficient of effective height of cross-section k = 1 + √(200 / d) ≤ 2
ρ_l	ratio of tensile reinforcement ρ_l = A_sl / (b_w ∙d) ≤ 0,02
f_ck	characteristic compressive cylinder strength of concrete
k₁	coefficient for calculation V_Rd,c loaded from Manager for National annexes
σ_cp	stress caused by axial force (N_Ed > 0 for compression) σ_cp = N_Ed / A_c ≤ 0,2 ∙ f_cd
b_w	the smallest width of the cross-section in tensile area of cross-section perpendicular to direction of resultant shear force, see "Width of cross-section for shear check"
d	effective depth of cross-section recalculated to direction of shear forces resultant, see "Effective depth of cross-section for shear check"
A_sl	tensile area of reinforcement
N_Ed	the axial force in the cross-section due to loading or prestressing.
A_c	the area of concrete cross section
f_cd	design value of concrete compressive strength
ν_min	Coefficient of minimum value of shear resistance of the member without shear reinforcement loaded from Manager for National annexes,see equation 6.3N in EN 1992-1-1
f_cvd	the concrete design strength in shear and compression, see equations 12.5 and 12.6 in EN 1992-1-1 if σ^ccp ≤ σ_c,lim: f_cvd = √(f_ctd² + σ_ccp ∙ f_ctd) if σ^ccp > σ_c,lim: f_cvd = √(f_ctd² + σ_ccp ∙ f_ctd - ((σ_ccp - σ_c,lim) / 2)²)
f_ctd	design axial tensile strength of concrete
σ_ccp	normal (axial)stress of uncracked cross-section σ_ccp = N_Ed / A_cc
σ_c,lim	limit value of stress caused by axial force, see equations 12.7 in EN 1992-1-1 σ_c,lim = f_cd - 2 ∙ √(f_ctd ∙ (f_ctd + f_cd))
A_cc	compressed concrete area for uncracked cross-section
V_Ed,max	maximum value of shear force resultant calculated without reduction by coefficient β, see clause 6.2.2(6) in EN 1992-1-1
b_w1	minimum width of cross-section between tension and compression chord perpendicular to direction of shear force, see "Width of cross-section for shear check"
ν	strength reduction factor for concrete cracked in shear loaded from Manager for National annexes, see equation 6.6N in EN 1992-1-1
V_Rd,max	the design value of the maximum shear force which can be sustained by the member, limited by crushing of the compression struts
α_cw	coefficient taking into account state of the stress in the compression chord, see note 3 in clause 6.2.3(3) in EN 1992-1-1. The value 1 is always taken into account for non -prestressed structures
z	inner lever arm of cross-section recalculated to direction of shear forces resultant, see "Inner lever arm for shear check"
ν₁	strength reduction factor for concrete cracked in shear loaded from Manager for National annexes, see note 1 and 2 in clause 6.2.3(3) in EN 1992-1-1. if σ_swd > 0,8 ∙ f_ywk : ν₁ = ν if σ_swd ≤ 0,8 ∙ f_ywk and f_ck ≤ 60 MPa: ν₁ = 0,6 if σ_swd ≤ 0,8 ∙ f_ywk and f_ck > 60 MPa: ν₁ = 0,9 - f_ck / 200 > 0,5
θ	Angle between concrete compression strut and beam axis perpendicular to the shear force, see "Angle between concrete compression strut and beam axis"
σ_swd	is design stress of the shear reinforcement σ_swd = V_Ed ∙ s / (z ∙ (cot θ + cot α) ∙ sin α)
V_Rd,s	design value of the shear force which can be sustained by the yielding shear reinforcement.
A_sw	the cross-sectional area of the shear reinforcement calculated as average area from all stirrups within calculated interval, see "Calculation of average characteristics of shear reinforcement"
s	the spacing of the stirrups calculated as average area from all stirrups within calculated interval, see "Calculation of average characteristics of shear reinforcement"
f_ywd	the design yield strength of the shear reinforcement. f_ywd = 0,8 ∙ f_ywk and σ_swd ≤ 0,8 ∙ f_ywk
α	angle of shear reinforcement . The angle of stirrups is always perpendicular (90 °) to member axis in SCIA Engineer
f_ywk	characteristic yield strength of the shear reinforcement
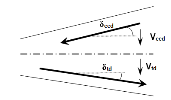
V_td	the design value of the shear component of the force in the tensile reinforcement, in the case of an inclined tensile chord
V_ccd	the design value of the shear component of the force in the compression area, in the case of an inclined compression chord

For member with inclined chords the additional forces haves to be taken into account for shear check according to clause 6.2.1(1). The calculation is prepared for taking into account also inclined chords. Nevertheless the calculation itself is not implemented yet. The partial components are explained in the following figure.