FEM - Neglecting of the moments of inertia of the beam members
Introduction
This chapter is to provide a closer information about change originated from the FEM solver implemented in SCIA Engineer version 24.0. The moments of inertia (rotational mass components) based on the self-weight of the beam members are now neglected. Examples are provided below. The reason of this change is to avoid certain unrealistic mode shapes (usually higher frequency modes), and to be in alignment with other finite element solvers (where the same logic is often implemented).
This change is applicable for modal analysis.
Example of cantilever beam of one finite element
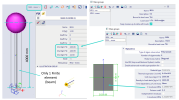
An example of this behaviour is shown considering a cantilever beam (column), consisting of one single beam finite element, hence, only two nodes (FEM nodes), where the bottom node is fully constrained, and the top node is free in all 3 translational and rotational directions.
Two mass groups are defined:
MG1 = mass generated from self-weight of the beam
MG2 = additional mass in the upper node, where translational masses in all 3 directions are 0, and only moments of inertia Imx, Imy and Imz are defined (the values are set to consider what is now neglected for this case)
Two combination of mass groups are defined:
CM1 = 1 × MG1 + 1 × MG2
CM2 = 1 × MG1
Below is the comparison of the solver before version 24.0, and since version 24.0
#A - (before v 24.0) Rotation around global X,Y,Z axes (moments of Inertia Imx, Imy and Imz) are neglected, in both cases, automatically generated from self-weight (MG1), and user-defined moments of inertia (MG2). Hence, there is no mass in the upper node that could rotate, therefore only 3 eigenmodes are possible to be calculated (3 DoF).
#B - (before v 24.0) Rotation around global X,Y,Z axes (moments of Inertia Imx, Imy and Imz) are considered, for both mass groups, MG1 based on self-weight, and MG2 where defined by the user. Hence, in this case for CM1, these moments of inertia are considered two times. For CM2, these are considered only once (within MG1). For this case, up to 6 eigenmodes might be calculated.
#C - (since v 24.0) Rotation around global X,Y,Z axes (moments of Inertia Imx, Imy and Imz) are neglected. This setting is now applicable for the user defined moments of inertia, hence for MG2, as the moments of inertia for MG1 (self-weight) are always neglected. This is practically the same as case #A.
#D - (since v 24.0) Rotation around global X,Y,Z axes (moments of Inertia Imx, Imy and Imz) are considered,. This setting is now applicable for the user defined moments of inertia, hence for MG2, as the moments of inertia for MG1 (self-weight) are always neglected, no matter the state of this setting. For this case, for CM1, up to 6 eigenmodes might be calculated, but for CM2 only up to 3 eigenmodes.
Below is the detail for case #Band #D when 6 eigenmodes are calculated (maximum number of eigenmodes for this model case).
Graphical depiction of the eigenmodes of the case #D for CM1 is in the figure below.
Graphical depiction of the eigenmodes of the case #D for CM2 (only MG1 from self-weight) is in the figure below. There are no rotational modes for this single case, as in the single node there are no moments of inertia.
Note: Be aware that in this example above, there is only one single unconstrained node (at the top of the column). Hence, in order to capture higher frequencies (e.g. those eignemodes 3, 4 and 5 from the CM1), finer mesh needs to be considered.
This example appears to reduce the number of eigenmodes significantly at the first glance. However, under normal circumstances, structure of many finite elements and nodes will be modelled, where reduction of these moments of inertia helps in removing of some unrealistic eigenmodes of higher frequencies. See example on larger structure below.
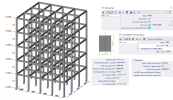
Example of a frame structure
This example shows what difference might user encounter as a consequence of the introduced change. Example is for simple concrete frame structure of geometry depicted in the figure below. Lanczos method and 50 eigenmodes are selected to be calculated.
There is only one combination of mass group CM1, which contains only one mass-group MG1 which is based on mass from self-weight.
#E - (before v 24.0) Rotation around global X,Y,Z axes (moments of Inertia Imx, Imy and Imz) are considered
#F - (before v 24.0) Rotation around global X,Y,Z axes (moments of Inertia Imx, Imy and Imz) are neglected
#G - (since v 24.0) For this case where there is only mass from self-weight, no matter whatether the rotation around global X,Y,Z axes (moments of Inertia Imx, Imy and Imz) are considered or neglected, the result is the same as for the case #F. There are rather negligible differences in frequencies, mostly only in the eigenmodes of larger frequencies.
Recommendations
If there are moments of inertia (Imx, Imy, Imz) defined within the nodal mass, do not forget to check the consideration of "Rotation around global X,Y,Z axes" is on. If off, there will be a warning to notify the user about this.