Internal forces in physically orthotropic plates

Technical theory of plates with the effect of transverse shear taken into account

This is what is termed as the Kirchhof theory of thin plates, based on formulas (4) and valid approximately within the range of

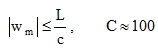
	(10)
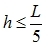
	(11)

where:

w_m

the maximal plate deflection

the plate thickness

the characteristic plate dimension in plan-view,

L = diameter of a circular plate, L = the shorter side of a rectangular or rhomboid plate, etc.

The consequences of failing to comply with (10) are:

Stress of significant intensity appears in the mid-plane of the plate, plane stress is added to the plate stress. We talk about geometrically non-linear plates with large deflections. Only tensile stress appears in the limit point h → 0, the plate becomes a membrane under tension (film of pneumatic structures, three-dimensional geometrically non-linear problems).

The consequences of failing to comply with (11) are:

For h > L/5, we get thick plates with a significant influence of transverse shear on the overall energy, deformation and stress-state of the plate, see paragraphs 5.2 and 6.3.

When conditions (10) and (11) are met, we define the following internal forces: Bending moment (subscript = the direction of reinforcement) in [Nm/m]:

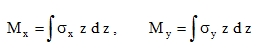
(12)

Torsional moment in [Nm/m]:

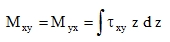
(13)

Shear forces in [N/m]:

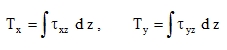
(14)

They are ignored over the thickness of the plate in the interval –h/2 ≤ z ≤ h/2. Considering the hypothesis (4), geometric conditions

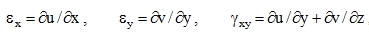
(15)

physical relation (9) and conditions of moment equilibrium of a plate element around x- and y- axis, we get formula (1) in the following form:

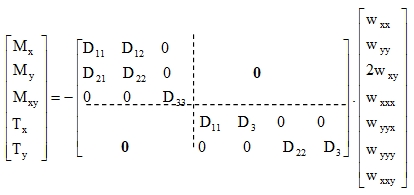
(16)

with the following elements of stiffness matrix D:

(●) Flexural stiffness:

(17)

(●) Contraction stiffness:

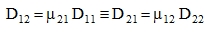
(18)

(●) Torsional stiffness:

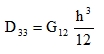
(19)

(●) Mixed stiffness:

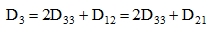
(20)

In total, we need five entries for matrix D: h, E₁, E₂, G₁₂, μ₁₂. The second coefficient of transverse contraction in the x-direction with the elongation in the y-direction is

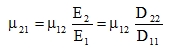
(21)

This number of entries can be reduced to four if we accept the assumption that a relationship similar to that valid for isotropy can be applied to shear modulus G₁₂, even though for geometric averages, see (39) below (another derivation was already presented by M. T. Huber):

(22)

Therefore, torsional stiffness D₃₃ is no longer an independent constant, but, following from (19) and (17), it can be expressed as

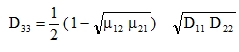
(23)

which can be written using (21) in the form:

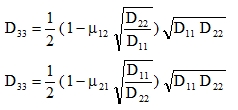
(24)

Formula (20) represents a coefficient at mixed derivation in the main equation for plates

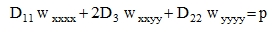
(25)

and is decisive for the type of orthotropy defined by constant

(26)

In the civil engineering practice, also the type (0 ≤ κ < 1) is usual. Sometimes we can meet the second type (κ = 1) that can be reduced to an isotropic solution. The third type (κ > 1) can appear only rarely in steel plates with closed ribs that are rigid in torsion.

Orthotropic constant κ can be, in certain types of plates, considered a primary piece of data that has been verified in practice and that represents the mixed stiffness of the plate

Thus, using (20) and (23), we can obtain the contraction stiffness in the form

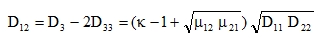
(27)

Usually, for κ = 1 we get

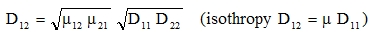
(28)

Plate reactions Q_x, Q_y are equal to shear forces T_x, T_y (similarly to beams) only if torsional moments M_xy at the edge are equal to zero (e.g. fully fixed edge). Generally, e.g. in a simply supported edge, the complement due to torsion must be added:

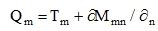
(29)

where m ^ n is either x ^ y or y ^ x or any other direction of the edge n with normal m. If the reactions are not calculated, they can be obtained from presented results with the derivatives calculated approximately by means of two adjacent values, e.g. in a sequence of equidistant border points 1, 2, 3 with step d:

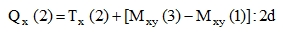
(30)

Plates with the effect of transverse shear taken into account

In the classical theory of plates that was discussed in the previous paragraph, shear moduli G₁₃, G₂₃ from (9) have no effect as the shear forces (14) are determined from the condition of moment equilibrium of the element, which leads to the last two lines of matrix (16). In thick plates and within the range of approximately

L / 5 < h < L ,

(31)

the right angle between the normal and the mid-plane of the plate is skewed by γ due to transverse shear τ_xz, τ_yz and, following from (4), the second and third line are eliminated. Then, according to (2) we have three independent functions w, ϕ_x, ϕ_y. Under such conditions, the following formulas are considered

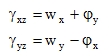
(32)

together with the fourth and fifth line of matrix (9). Therefore, instead of matrix (16) we get the matrix:

(33)

with new elements that, for the simplest configuration of a constant transverse shear across the plate thickness h, are:

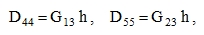
(33)

and consequently, the five entries h, E₁, E₂, G₁₂, μ₁₂ are extended by two more: G₁₃, G₂₃, which means in total seven entries for the calculation of input data for D.