Output of deformations on absent members

Symptoms

The following error message may appear in Steel code check results, when absences are used:

E-ABS01: Absences cause wrong deformation results on absent entities. Deformations on non-absent entities are correct. Internal forces are correctly taken into account for all entities.

What actually means:

Explanation

The structural analysis is carried out by the FEM solver using displacement-based finite elements. That is the most common finite element theory in structural analysis software. Because of that, displacements are always calculated in the nodes of the structure. That is where the issue in deformation results of absent members is coming from.

Essentially, an absent member has no results, as it is not included in the analysis model for the considered load case. However, it may happen, that an end node of an absent member is connected to another member what is not absent. In such as case, displacement results are available in that end node, although the absent member is not included in the analysis.

As deflections in 1D members are interpolated from displacements values in the nodes that are linked to them, deformations in an absent member may be interpolated from values that are irrelevant for that member, leading to incorrect deformation results along the member.

Internal forces, on the other hand, are always computed first at integration points, located inside each finite element - not at the end nodes. As a consequence, when a member is absent from the model the corresponding integration points are also absent and internal forces are simply not calculated for that member. It follows, that internal forces are systematically zero for an absent member.

Example

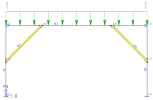
Analysis model of sample structure

Two load cases are applied to the structure, with the same line load.

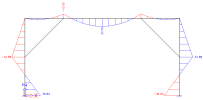
As explained, internal forces for both load cases are consistent. For LC1, without absences:

Internal forces My and N for load case LC1

And for LC2, with B4 and B5 absent:

Internal forces My and N for load case LC2

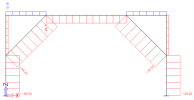
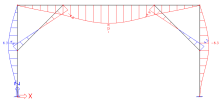
Deformations on beams for LC1, without absences, are also fully consistent:

Deformation uz on beams for LC1, without absences

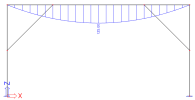
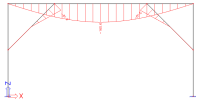
For load case LC2, where beams B4 and B5 are absent, deformations on beams are correct for B1, B2 and B3, which are not absent. But there are inconsistencies for absent members B4 and B5:

Deformation uz on beams for LC2, with absences on B4 and B5

As B4 and B5 are absent in LC2, results should be zero on those two members. But it is not the case. Why?

Because the local beam displacements are interpolated from node displacements.

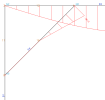
Consider B4 and its mesh:

Mesh details and deformations on beam for member B4 and load case LC2

B4 has 3 mesh nodes (because of applied mesh refinement - 2 tiles per member).

The results at the node in the middle of the member (mesh node 16) are zero, because the node is connected only to B4 and is, therefore, also absent from the calculation of LC2.

The other two nodes, N5 and N6, are connected to B1 and B2, respectively. B1 and B2 are not absent for LC2. As a consequence, there can be non-zero displacement results in those two nodes for LC2. As a matter of fact, the results are clearly non-zero at node N6.

SCIA Engineer interpolates the displacements along the beam from the available nodal values, which leads to the output above.

Those results are not directly usable to obtain correct displacement values in B4. Neither absolute, not relative deflections. Also, a check of allowable deflection based on those results would also lead to wrong conclusions.

Solution

In order to obtain correct displacement results, as well as correct SLS deflection checks, results must be displayed separately for members that are absent and for members that are not.

For members, that are not absent, just use normal output or checks. Simply make sure, that only members without absences are selected for output.

For members that are absent for one or more load cases in the selected combination, do the following: