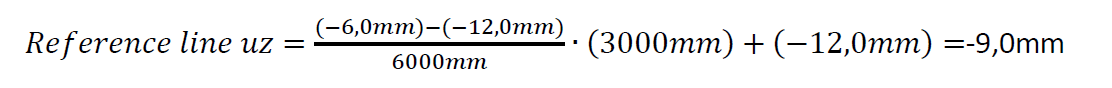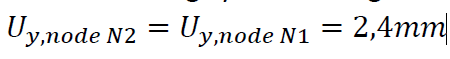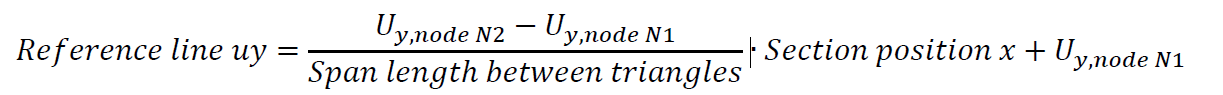1D Relative deformations

Relative deformations can be found under 1D Deformation result service.

Theory

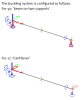
Relative deformation is the distance from reference line to deformed shape. There are two configurations how the relative deformations can be calculated - standard and cantilever. These configurations are based on buckling data. See example below which describes both cases.

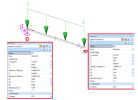
An IPE270 beam with a length of 6m is supported on its end nodes with hinged supports which are flexible in the Z-direction. Two line loads: qz = -20,0kN/m and qy = 2kN/m.

$image\truncatedcone.gif$

The buckling system is configured as follows.For yy: ‘beam on two supports’; For zz: ‘Cantilever’

$image\truncatedcone.gif$

Relative deflection uz calculation - standard:

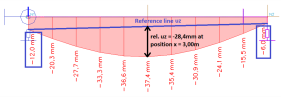
Absolute deformations uz can be seen in the picture below. Because the buckling system yy has two

fixed buckling supports we can construct the reference line as the line between these two nodes.

$image\truncatedcone.gif$

The reference line can be calculated if the absolute deformations of the fixed (buckling)supports are

known. In node N1 -> uz = -12,0mm and in node N2 -> uz = -6,0mm.

The function which describes this reference line can then be obtained:

$image\truncatedcone.gif$

Let’s calculate the value of the reference line in the middle (pos.x = 3,00m) by using the above

mentioned formula:

$image\truncatedcone.gif$

The relative deformation is then the substraction between the absolute deformation at position x

and the the uz-value of the reference line.

Relative deflection uy calculation - cantilever:

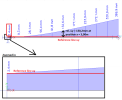
Absolute deformations uy can be seen in the picture below. Because the buckling system zz has only

one fixed buckling support the reference line should be constructed starting from the fixed support

and parallel with the member system line.

$image\truncatedcone.gif$

The reference line can be calculated if the absolute deformations of the fixed (buckling)support is

known. In node N1 -> uy = 2,4mm. An additional step needs to be done for cantilever configurations

namely: apply the absolute deformation of the fixed node to all the other free nodes (i.e. nodes

without buckling supports) of that buckling system configuration zz in this case. This means the

following for this example:

$image\truncatedcone.gif$

Now we can re-use this formula for the reference line uy:

$image\truncatedcone.gif$

Let’s calculate the value of the reference line uy in the middle (pos.x = 3,00m) by using the above

mentioned formula:

$image\truncatedcone.gif$

The relative deformation is then the substraction between the absolute deformation at position x

and the uy-value of the reference line.