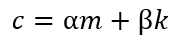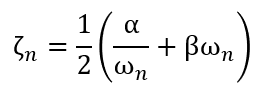Harmonic damping type - Rayleigh damping

When the Rayleigh damping is selected, each frequency is damped by a different damping ratio.

Theory

The model of Rayleigh damping approximates the damping coefficient c as a linear combination of stiffness and mass:

where α is the mass proportional damping (unit in 1/second) and β is the stiffness proportional damping coefficient (unit in seconds).

The damping ratio ζ (zeta) for the n-th mode is defined by:

The Rayleigh damping coefficients α and β can be determined based on two damping ratios ζ_i and ζ_j for the i-th and j-th mode ω_i and ω_j. In SCIA Engineer it is assumed, that both of these modes have the same damping ratio ζ, hence the α and β are obtained from the equations:

where ω_i and ω_i are two considered angular frequencies (ω = 2 π f).

Example of input

In example below, the input parameters for Rayleigh damping are set as:

damping ratio ζ = 3%

two reference frequencies f₁ and f₂ are considered as 1 and 10 Hz respectively.

This means, for these two reference frequencies (f₁ < f₂), the damping ratio will be equal to the input value of the 3%. For all frequencies in the range (f₁ , f₂), the damping ratio will be slightly smaller, and for frequencies below f₁ and above f₂, the damping ratio will be larger. This is graphically depicted in the figure below.

The Rayleigh damping parameters are calculated according to the equations above, and informatively provided in the corresponding properties by the greyed-out values.