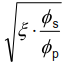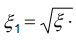Theoretical background
Cracking status
Before calculation of crack width the normal concrete stresses on un-cracked section at the most tensioned fibre has to be checked. If condition below is satisfied, the crack width does not create and the crack width is not calculated
σct ≤ fct,eff
where
There cracking forces (Ncr, Mcry, Mcrz) are also presented in the in table output. These cracking forces are forces which cause the reaching of value fc,teff (occurring of crack width in cross-section) in the most tensioned fibre of concrete cross-section in direction of first or second principal stress. For calculation of this cracking forces is used condition, that eccentricity of inputted forces and cracking forces has to be the same.
Effective modulus of concrete
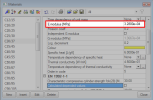
This value can be set in Concrete setting by using Advanced level or in 1D member data (advanced mode is ON). If this check box is ON, then effective module of elasticity is taken into account.
EN 1992-1-1 does not give instruction how creep under varying load should be taken into account for calculation of the crack width. The creep can be generally taken into account by assuming that effective module of elasticity (EN 1992-1-1, clause 5.8.7(2) ) for calculation modular ratio (Es/Ec,eff ≈ 15). A Lower value of modular ratio (greater value of module of elasticity of concrete than effective ) may be used where less than 50 % of the stresses arise from quasi-permanent load. The different value of modulus of elasticity can be input directly in material properties, see picture below, but these changes has influence to FEM analysis too.
Calculation of crack width
The crack width is calculated according to EN 1992-1-1, formula 7.8.
w = sr,max • (εsm - εcm)
where
| sr,max | maximum crack spacing |
| (εsm - εcm) | difference between mean strain in the reinforcement and the mean strain in concrete between the cracks |
Difference between mean strain in the reinforcement and the mean strain in concrete between the cracks
Difference between mean strain in the reinforcement and the mean strain in concrete between the cracks is calculated according to EN 1992-1-1, formula 7.9
where
| σs | the stress in the most tensioned reinforcement |
| Es | design value modulus of elasticity of the most tensioned reinforcement member |
| kt |
factor dependent on duration of the load. If check box "Use of effective modulus of concrete" is ON, the value 0.4 is used, otherwise value 0.6 is used |
| fct,eff | is the mean value of the tensile strength of the concrete effective at the time when the cracks may first be expected to occur. |
| ρp,eff | ratio of reinforcement within effective area of concrete in tension |
| αe | ratio of design value of modulus of elasticity of the most tensioned reinforcement and modulus elasticity of the concrete |
From the formula above follows that difference between mean strain in the reinforcement and concrete mainly depends on:
- strain (stress) in the most tensioned reinforcement,
- effect of tension stiffening.
Strain in the most tensioned reinforcement
Strain in the most tensioned reinforcement is calculated according to formula below
There are used following preconditions in SCIA Engineer:
- The section is loaded by load/combination/class selected in service crack control,
- Transformed section is used
- Plane section remains plane after loading (deformation) too
- Tensile strength of concrete is not taken into account (cracked section)
- Ideal bond between concrete and reinforcement is taken into account, it means that change strain of reinforcement εs and concrete fibre εc in the same position is the same
- The linear strain-stress diagram of concrete and reinforcement with infinite branch is used, it means, that distribution of stress is linear and depends on change of strain (Hook’s law)
| Linear stress-strain diagram of concrete | Linear stress-strain diagram of reinforcement |
|---|---|
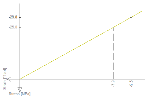
|
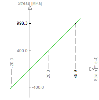
|
Effect of tension stiffening
The tension stiffening effect represents the capacity of the intact concrete between neighbouring cracks to carry a limited amount of tensile forces. The reason for this effect is bond slip between the reinforcement and the neighbouring concrete. The decreasing of stress in reinforcement due to tension stiffening can be calculated according to formula:
where
The program finishes with error if area of reinforcement As,eff is zero,
EN 1992-1-1 does not give instruction, how creep under varying load should be taken into account for calculation of the crack width. The creep can be generally taken into account by assuming that effective module of elasticity (EN 1992-1-1, clause 5.8.7(2) ) for calculation modular ratio (Es/Ec,eff ≈ 15). A lower value of modular ratio (greater value of module of elasticity of concrete than effective ) may be used where less than 50 % of the stresses arise from quasi-permanent load. The effective module of elasticity can be taken into account by check box Use effective modulus of concrete (see 2.1.3 ) .The different value of modulus of elasticity can be input directly in material properties, but these changes has influence to FEM analysis too.
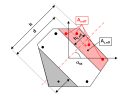
Maximum crack spacing
Maximum crack spacing is calculated according to EN 1992-1-1, clause 7.3.4(3)
where