Materials theoretical background

 

Characteristic basic residual values

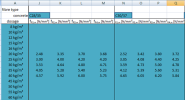
The calculation of material characteristics is based on the document see[1] DAfStb Guideline "Steel fibre reinforced concrete".The calculation of characteristic values is dependent on fibre type and dosage. Each concrete class has recommended fibre types and dosages. Based on that the residual strengths values f_R1,m to f_R4,m are determined. These strengths are input for other calculation. Nevertheless the characteristic values will be presented in the material library as the first values for user (f^f_ct0,L1; f^f_ct0,L2; f^f_ct0,u; f^f_ct0,s). The input for calculation is list of measured values from the tests. This list is available for specific concrete class, fibre type and dosage (see the example below).

Note: There are implemented material characteristics f_R1-4,m based on version 1.1.6 from Bekaert.

Then the following precondition is considered:

f_R1,m = f^f_cflm,L1

f_R4,m = f^f_cflm,L2

Next step is calculation of residual flexural strength from formula O.3 from German guideline (only limit value is used)

f^f_cflk,L1 = 0.51 ∙ f^f_cflm,L1

f^f_cflk,L2 = 0.51 ∙ f^f_cflm,L2

Then this strengths are used in formulas for characteristic values of residual tensile strength (see R.3.31-34) and will be visible in material library

f^f_cft0,L1 =f^f_cflk,L1 . β_L1

f^f_cft0,L2 =f^f_cflk,L2 . β_L2

f^f_ct0,u =f^f_cflk,L2 . β_u

f^f_ct0,s =f^f_cflk,L2 . β_s for L2/L1 ≤ 1,0

f^f_ct0,s =f^f_cflk,L1 . β_s for L2/L1 > 1,0

Beta factor calculation

Determination of beta factors (β_L1 and β_L2 is done based on figures P.1 and P.2 from see[1] DAfStb Guideline "Steel fibre reinforced concrete"

β_L2 = 1 / 3 ∙ L2/L1 + 0,02

when

0,7 ≤ L2/L1 ≤ 1,0

or

β_L2 = 0,18 ∙ L2/L1 + 0,17

when

1,0 ≤ L2/L1 ≤ 1,5

Determination of beta factors β_s and β_u

β_u = 0,37; for the stress block

β_s = 0,37; when using reinforcement

When ratio L2/L1 is mentioned in the text above it means ratio of f_R4,m / f_R1,m is used

Residual values

The second step of calculation material characteristic is calculation of residual values from characteristic ones. Member size and fibre orientation are another items affecting the calculation The simplification is done by taking into account values

κfG	member size effect; there will be one factor per material and for slab = 1,7
κfF	fibre orientation effect = 1,0 for bending and tensile loads = 0,5 for shear

Both values will be possible to edit in material library per specific material. Additionally, there will be two values for κ^f_F (general and for shear only) - see[1] DAfStb Guideline "Steel fibre reinforced concrete".

Then residual values of material characteristics are calculated using the following formulas (see R.3.36-39):

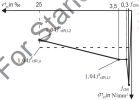
f^f_ctR,L1 = κ^f_F ∙ κ^f_G ∙ f^f_ct0,L1

f^f_ctR,L2 = κ^f_F ∙ κ^f_G ∙ f^f_ct0,L2

f^f_ctR,u = κ^f_F ∙ κ^f_G ∙ f^f_ct0,u

f^f_ctR,s = κ^f_F ∙ κ^f_G ∙ f^f_ct0,s

Design values

The third step of calculation material characteristic is calculation of design values from residual ones.

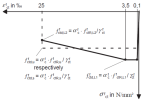
f^f_ctd,L1 = α^f_c . f^f_ctR,L1 / γ^f_ct

f^f_ctd,L2 = α^f_c . f^f_ctR,L2 / γ^f_ct

f^f_ctd,u = α^f_c . f^f_ctR,u / γ^f_ct

f^f_ctd,s = α^f_c . f^f_ctR,s / γ^f_ct

 

where

αfc	reduction factor which is aligned with the design concept of this document to allow for long-term effects on the residual tensile strength of steel fibre reinforced concrete (see[1] DAfStb Guideline "Steel fibre reinforced concrete") = 0,85
γfct	partial safety factor according to Table R.1 (see[1] DAfStb Guideline "Steel fibre reinforced concrete") = 1,25

Material diagrams

The material diagrams are completely different than standard concrete material diagrams. The effect of fibres are taken into account by tensile branch. Here just behaviour in tension is described

There are two types of material diagram used in analysis dependent on analysis type:

• diagram for linear analysis and section design - this diagram is based on design values

• diagram for nonlinear analysis - this diagram is based on residual values