Slab displacement and curvature

Parameters

Name	Defines the name of the load. It may facilitate the identification of the load.
Epsilon [mm/m’]	Relative elongation due to increase of temperature or shrinkage.
k [mrad/m’]	Curvature of the plane due to non-uniform increase of temperature or shrinkage.

A little bit of theory

Considering that the material is homogenous and isotropic and that the temperature is distributed linearly across the member thickness, the elongation of a member due to the increase of temperature can be easily calculated.

Let’s assume increase of temperature at the upper surface TH and increase of temperature at the lower surface TD. The final increase of temperature (shrinkage) can be divided into two components – see the figure below.

Considering this, we obtain:

Elongation (in m/m’)

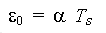
where

alpha	coefficient of thermal expansion
Ts	the increased temperature

Positive increase of temperature gives positive value of elongation.

Curvature

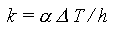
where

alpha	coefficient of thermal expansion
delta T	difference in temperature between the surface z = -h/2 and z = +h/2.
h	member thickness

It follows from geometry that k = 1 / R, where R is a radius of a spherical surface the shape of which the members takes if the change of shape due to an increase of temperature is not prevented.

Note: If the increase of temperature is not linear across the member, the distribution of temperature increase must be linearised. The results must be then revised and stress resulting from the difference between the given and linearised increase of temperature must be obtained by a special calculation and added to this result.

Example

Imagine the following – rather theoretical – situation. Let’s have a circular slab supported in its centre only.

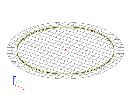
First, let’s subject this slab to the uniform elongation of 10 mm/m. It is possible to imagine that both surfaces of the slab are heated.

After calculation, we may see the overall and symmetrical expansion of the slab (the figure shows both the original slab and the deformed finite element mesh).

 

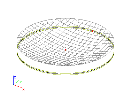
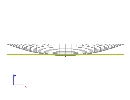
Second, let’s subject the slab to non-uniform expansion (curvature) of 10 mrad/m. It is possible to imagine that only one surface of the slab is heated.

After calculation, we may see the bowl-like deformation of the slab that results from this type of load. The figure shows the both the original slab and the deformed finite element mesh. The second figure presenting the side-view is more illustrative.