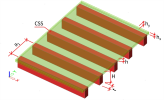
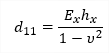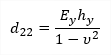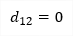3 Type “Slab with ribs”
This is a special type for thick plates without transverse contraction.
The user is able to input cross-section in the x-direction from library of cross-sections or via direct input of rib properties.
There are two options for the rib:
Rib type “CSS lib”
– the user is asked to select a cross-section from library and spacing between the cross-sections

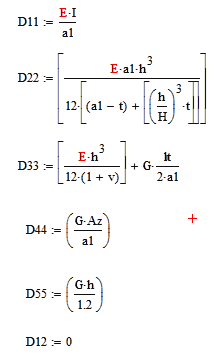
The formulas for Dij parameters include also possible diverseness Ex ≠ Ey [Nm-2]. Properties of ideal T-section are taken into account in the case of Ex ≠ Ey. The centre of gravity of an ideal T-section is calculated and cross-section is transformed to a cross-section with one E modulus.
Case 1: The E modulus of the cross-section (E1) is greater than E modulus of the slab (E2)
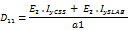
Case 2: The E modulus of the rib (E1) is lower than E modulus of the slab (E2)
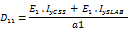
Model Slab with ribs takes into account the flexural stiffness of the T-section (cross-section + slab). Model One direction slab calculates only with sectional properties in the x-direction!
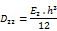
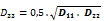
The following properties are taken from sectional and slab properties:
| E1 | modulus of elasticity of cross-section [ MPa ] |
| E2 | modulus of elasticity of slab [ MPa ] |
| IyCss | moment of inertia of cross-section [ m4 ] |
| IySlab | moment of inertia of slab [ m4 ] |
| a1 | distance between 1D members [ m ] |
The last two parameters are related to the shear stiffness of the cross-section and slab. D44 and D55 are considered in the sense of the Mindlin model.

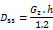
| Az1 | effective surface for shear of cross-section [ m2 ] |
| G1 | modulus of elasticity of cross-section [ MPa ] |
| G2 | modulus of elasticity of slab [ MPa ] |
Membrane orthotropy
Rib type “Input“
– the user is asked to input the dimensions of the rib (T-section) and spacing between the ribs
| E | modulus of the material |
| I | moment of inertia of a T section of width a1 |
| Az | shear surface of a T section of width a1 |
| h / H | torsional rigidity of the rib |
| t | rib thickness |
| h | .slab height |
| (H-h) rib | depth |