3 Type “Two heights”

This is a special orthotropic continuum for 2D structures of Mindlin type (thick plates). The basic idea follows from the engineering idea of a 2D reinforced concrete member, the stiffness of which can be principally derived from two (generally different) member heights h₁, h₂ in two characteristic / principal orthotropic directions (x, y)_p. The values of h₁ and h₂ can be derived from a more or less sophisticated numerical reformulation of a geometric orthotropy which appears, for example, in plates stiffened by ribs, or they can represent an approximation of the behaviour of a 2D member in cracked state near its bearing limit (in German literature is it is called State II of a reinforced continuum) which makes the different reinforcement percentages in both directions the main stiffness characteristics (instead of the gross concrete section in the linear State I).

Mathematical description of orthotropy model

Flexural orthotropy

The formulation of a flexural orthotropic continuum is based on flexural stiffnesses of the Kirchhoff type in the principal orthotropy directions:

Flexural stiffness in direction x_p [MNm/m]     (1) 

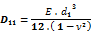
Flexural stiffness in direction y_p [MNm/m]  (2)

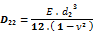
Transverse contraction x_p — y_p [MNm/m]  (3)

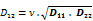
Torsion stiffness related to (x,y)_p [MNm/m]  (4)

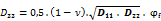
Shear flexural stiffness in direction x_p [MN/m]  (5)

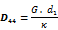
Shear flexural stiffness in direction y_p [MN/m]    (6)

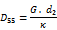
Membrane orthotropy

In the Wall model the membrane stiffnesses (4 parameters) play the role of the flexural ones in the Plate model. The most general Shell model defines both parameter sets simultaneously (in total 10 orthotropy parameters):

 

Normal membrane stiffness in direction x_p [MN/m]  (7)

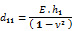
Normal membrane stiffness in direction y_p [MN/m]  (8)

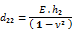
Transversal contraction x_p—y_p [MN/m]  (9)

Shear membrane stiffness related to (x,y)_p [MN/m]  (10)

 

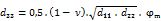
Symbols in flexural formulae (1) – (6):

d1, d2	Statically effective cross-section heights in orthotropy principal directions (x, y)p in flexure resistance
E	Module of elasticity of the reinforced concrete continuum
ν	Poisson’s coefficient of transverse contraction (ν1 = ν2 assumed generally)
G = E / (2.(1+ν))	Shear module of elasticity of the reinforced concrete continuum
κ = 1.2	Shear reduction coefficient for rectangular cross-section (may also be set κ= 1.0)
ϕf	Torsion reduction coefficient; using ϕf — 0 so called “torsion-week” Plate models can be simulate providing reduction of lifting corner forces as well as the lower/upper corner main reinforcement

Alternatively applied symbols in the membrane stiffness formulae (7) – (10):

h1, h2	Statically effective cross-section heights in orthotropy principal directions (x,y)p for membrane resistance. For example, the gross cross-section height in one orthotropy direction, modified in the other direction etc.
ϕm	Membrane shear reduction coefficient; using ϕm — 0, the so called “shear-week” wall models can be simulated, e. g. aimed at excluding such members (maybe masonry walls!) from the horizontal stiffening system of the construction

Discussion of the formulae (1) – (6):

(1) Parameters D₁₁ (1) and D₂₂ (2) are what is known as Kirchoff flexural stiffnesses and are thus self explanatory. Symbols d₁ and d₂ represent some characteristic heights associated with the principal orthotropy directions, e.g. the cross-section height(s) (both or one of them modified) or the statically effective heights of the two conjugated slab directions or other values;

(2) Shear stiffnesses D₄₄ (5) and D₅₅ (6) are related, in the sense of the Mindlin model, merely to the cross-section area and not to the effective shear height, which is usual in most shear proof procedures. In the present orthotropy model it is assumed that formulae (4), (5) use the same reference heights d₁ and d₂ as the flexural stiffness formulae (1) and (2);

(3) D₃₃: this is the most discussed stiffness parameter. If D₃₃ is reduced by means of ϕ_f, the torsion stiffness of the slab diminishes relatively to the coordinate axes, which are also the principal orthotropy axes. D₃₃ = 0 signifies a complete lack of torsional stiffness; such a slab can resist any torsion moments m_xy. Thus, no Kirchhoff’s lifting corner forces can develop; this phenomenon may be the primary reason for use of such class of models. As a fact, SCIA Engineer does not allow the user to set any exact zero value. However, values till 5 % (ϕ_f = 0.05) have proven to yield numerically stable results. It means that there ought to be set a lower input limit for ϕ_f in the SCIA Engineer input control procedure.