Averaging strips

This functionality provides for automatic averaging of peak results around defined points or along defined line strips on slabs. The users can define several styles how to calculate the averaged values. The averaging can be applied to internal forces on slabs and to required reinforcement areas used in the design of reinforcement in concrete slabs.

The averaging strips are defined as what is termed additional data. This fact together with some other characteristics of the averaging strips leads to the following rules concerning the manipulation with the already defined strips:

• No geometrical manipulation is supported (i.e. the averaging strip cannot be copied, moved, etc.) The only exception is the direct editing of the coordinated of the definition points in the Property Window.

• The averaging strip can be normally deleted.

• The removal or editing of the defined averaging strip DOES NOT influences the results.

• If the slab that contains the averaging strip is moved, copied, etc. the averaging strip "goes with" its master slab.

• The averaging strips react to the activity of the slabs. It means that only averaging strips that are defined on active slabs are visible.

• Check of data verifies the position of the strips and all invalid strips (e.g. located out of the master slab) are deleted.

Averaging strips versus finite element mesh

The averaging algorithm uses only the FE nodes that are located inside the averaging strip. This may cause certain inaccuracies especially in the combination with larger finite elements. Therefore, it is recommended to define internal edges along the averaging strips. This ensures that finite element nodes are generated along the edge of the averaging strip, which may significantly improve the accuracy.

The recommended procedure is thus:

1. Define the model of the structure.

2. Perform the calculation.

3. Review the results.

4. Define averaging strips.

5. Review the averaged results.

6. Decide on the final location and number of averaging strips.

7. Define internal edges along the averaging strips.

8. Repeat the calculation to obtain the improved results.

"Density" of averaging strips

The averaging strips can be defined almost arbitrarily. For the purpose of this paragraph we will distinguish two situations. Averaging strips defined with a gap between individual strips and averaging strips defined one next to another (e.g. strip above support and strip in the "middle" of the span defined without any gap in between).

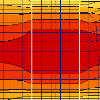
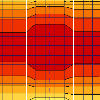
The possible effect of these configurations can be best explained in the following pictures.

Separate strips (i.e. gap between strips)

If the averaging strips are defined as separate, the algorithm can meet the condition that the distribution of the quantity should as much constant across the span as possible. In other words, the quantity is constant (more or less) across the whole width of the strip. The vertical white line indicates the strip.

Adjacent strips (i.e. no gap between strips)

On the other hand, if the averaging strips are defined closely one next to another, there is no space between them for the algorithm to handle the change of the magnitude of the given quantity, as the magnitude cannot change in step, it must be gradual. Thus one of the strips must be affected by the change in the magnitude. This is shown in the figure below where the value of the result quantity varies along the width of the strip.

In averaging strip only basic values (mx, my, mxy, vx, vy, nx, ny, nxy) are always averaged, principal and other values (e.g. required areas of reinforcement in concrete checks) are always calculated using these averaged basic values. Each value has some direction (e.g. mx act in the direction of x axis) and it is averaged only in the perpendicular direction, i.e. mx is averaged only in y direction.

Averaging strip, which is rotated towards LCS of the slab, is useful e.g. in case of slant line support. In the first step the basic values are transformed to rotated coordinate system of averaging strip ("Angle" property), in this system they are averaged and then they are transformed back to LCS of the slab.

Averaging of mxy and vxy is slightly different. Averaged value is calculated in standard way but the signs are preserved, i.e.on part where the value has been positive there is average value with positive sign and vice versa. In addition, averaging of mxy and nxy is done in both directions (longitudinal and perpendicular), so if the averaging strip is also set to average in both directions ("Direction" property) the final value is constant across the whole strip (with respect to original signs).