Open topic with navigation

Shear Force

The Shear Force Check is executed according to EN 1993-1-3 art. 6.1.5.

General

The shear resistance is calculated for each ‘web’ element separately and the cross-section resistance is taken as the sum of these element resistances.

Only elements with element types I, UO and SO are accounted for.

In addition, elements with stiffener type RUO or DEF are not accounted for.

Formula (6.8) is rewritten as follows for both directions:

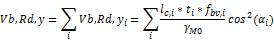
With:

α_i = Angle of element i related to the principal y-y axis

l_c,i = Centreline length of element i

By default the Shear Check is executed ‘without stiffening at the support’ In case Local Transverse Forces data are inputted which have the checkbox ‘No Local Transverse Forces Check’ activated, the Shear Check in those sections is executed ‘with stiffening at the support’.

Elements without Internal stiffeners

The centreline length l_c,i for each element i is taken from the Initial shape.

The angle α_i for each element i is determined as the angle related to the principal y-y axis.

The relative web slenderness for each element i is determined according to formula (6.10a).

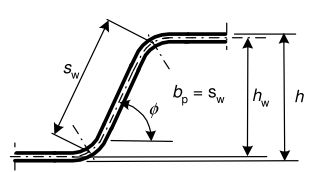
The slant height s_w,i is taken as the notional width b_p,i of the element under consideration as indicated on the following picture.

Sections with Internal stiffeners

Special considerations are required for cross-sections with internal stiffeners (Type RI).

The following picture illustrates a web with internal stiffener:

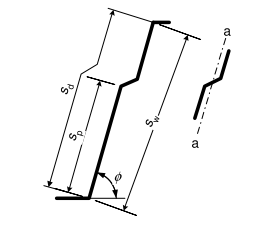
The internal stiffener and connected elements are seen as ‘one web’. This ‘composed’ web is seen as ‘one’ element i in the shear calculation.

For such a ‘composed’ web, the different distances are determined as follows:

• The slant height s_w is taken as the distance between
  - The starting point of the nominal width b_p,i of the first element in the web.
  - The end point of the nominal width b_p,i of the last element in the web.
• The total developed slant height s_d is taken as the sum of the nominal widths b_p,i of all the elements in the web.
• The slant height s_p concerns the notional width b_p,i of the largest plane web element.

The relative web slenderness is determined according to formula (6.10b).

The inertia of the stiffener(s) I_s is taken from the Initial shape

The centreline length l_c of this composed web is calculated as follows:

• In case the first or last element of the composed web has element type SO or UO:

l_c = s_w + g_r

With

g_r = r_m * [tan ( φ / 2) - sin ( φ / 2)]

If the first element is an outstand, g_r is taken as g_r at the end point of the last element.

If the last element is an outstand, g_r is taken as g_r at the starting point of the first element.
Reference is made to "Notional widths".

• In case both the first and last element of the composed web has element type I:

l_c = s_w + g_r,first + g_r,end

With

g_r,first taken as g_r at the starting point of the first element.

g_r,end taken as g_r at the end point of the last element.

The angle α of the ‘composed’ web concerns the angle of the centreline length l_c relative to the principal y-y axis.

Neighbouring connected elements are seen as one ‘web’. A typical example of this is a sigma section: the web has two internal stiffeners which both are connected to the same internal element. As such they are recognized as forming one web.

Open topic with navigation