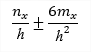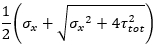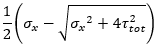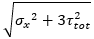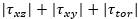1D stresses

The 1D internal forces command serves for displaying internal forces on selected 1D members. (not only on Beams, but also on Ribs, Tendons and Integration strips/members)

Usage

  1. Calculate a FEM analysis of the model
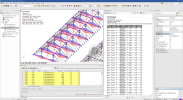
  2. Go to Tree > Results > Beams > 1D stresses
  3. Set properties of the command to specify mainly:
    • selection of 1D members where the results are evaluated
    • load type from which the results are derived
    • specific result value from the available list to be visualized
  4. Click on [Refresh] action button to display the results

Note: To get general overview about how to work with Result service and its commands, see Results/Basics.

Properties

Category Property Description / Notes
Selections

Type of selection

All / Current / Advanced / Named Selection

Specifies on what members the results are displayed

See "Type of selection"

 
Filter

No / Cross-section / Material / WildCard / Layer / Type of beam

Result case Type of load

Load case / Combinations / Classes / Nonlinear Combinations/ Stability Combinations / Mass combinations

Defines for what load the results are displayed.

See"Result case"

Extreme 1D Extreme 1D

Section / local / Cross-section / Design group / Member / Global

Defines the position where extremes of result value are evaluated.

 
Type of values

Basic magnitudes / Principal magnitudes

  
Values See table Values below.
 

Fibres

All / Top / Bottom / Named fibre / All named fibres

 

Cross-section parts

All / Named cross-section part

 
 

Consider torsion due to shear centre eccentricity

On / Off

With this option ON, the shear forces are considered to act in the centre of gravity and therefore the shear stresses are magnified by additional torsion effect from eccentricity of shear forces.

Shear stresses on 1D members are calculated by default from shear forces and torsion moment, where shear forces are considered to act in the shear centre of the beam's cross-section. In case of cross-section with different position of shear centre with respect to the centroid of gravity this approach leads to discrepancy in the position of acting forces. Typical example of such cross-section is hot-rolled U shaped cross-section.
 

Print combination key

On / Off

 

Results in sections

All / Selected

If results in sections is set on Selected, new possibilities are available

Ends / Close to middle / Inputted
Drawing Setup 1D   " Drawing setup 1D"
Errors, warnings and notes settings   "Errors, warnings and notes settings"

Values

The following categories of 1D stresses can be displayed:

Basic magnitudes

The basic stresses are default magnitudes referring to the local axes of the selected coordination system.

Value Description Notes
σx

normal stress in direction of local axis x

 It is calculated on assumption of linear distribution of the strain within the section. In the first step the plane of deformation is calculated using iterative algorithm () so strain in all fibres is known. In the next step adequate stresses are assigned using stress-strain curve. Remember that linear calculation uses linear approximation (E modulus) of stress-strain curve.
txy transverse shear stress from shear force Vy in direction of principal axis y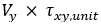

The shear stress components are calculated from the principal shear forces (Vy, Vz) and torsional moment (Mx) using relevant unit shear stress factors (τxy,unit, τxz,unit, τtor,unit) from Cross-section characteristics.

 
txz transverse shear stress from shear force Vy in direction of principal axis z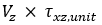
ttor shear stress from torsion moment Mx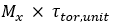

Principal magnitudes

The principal stresses represent the extreme values of the internal forces derived from the basic ones by transformation into the directions of principal axes:

Value Description Notes
σ1

maximum principal stress

 
σ2

minimum principal stress
σE

equivalent stress (von Mises)
ttot

total shear stress