Geometrical nonlinearity
Definition, application
The geometrically nonlinear analysis respects the conditions of equilibrium on a deformed structure. The SCIA Engineer program makes it possible to choose from 2nd order and 3rd order. Both variants represent an algorithm that is implemented in SCIA Engineer as a part of the standard FEM solver.
For taken into account it is necessary to perform " Nonlinear calculation".
Where to find it
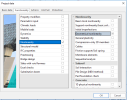
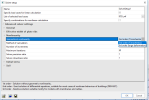
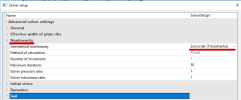
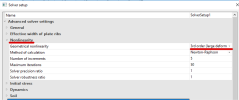
In project data dialog in part 'Functionality' it is necessary to switch ON 'Geometrical nonlinearity'. After that in solver setup for nonlinear analysis there is possibility 'Geometrical nonlinearity' where it is possible to select '2nd order (Timoshenko)' or '3rd order (large deformation)'.
Description / Background
1st order
Standard linear calculation, It may be used only when the displacement effects on the structural behaviour are negligible.
2nd order
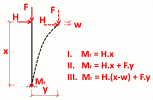
is called “Timoshenko method” which is based on the exact Timoshenko solution for members with known normal force. It is a 2nd order theory with equilibrium on the deformed structure which assumes small displacements, small rotations and small strains. The influence of the normal force on the bending stiffness and the additional moments caused by the lateral displacements of the structure (the P-Δ effect) are taken into account in this method. The method needs only two steps, which leads to a great efficiency. In the first step, the axial forces are solved. In the second step, the determined axial forces are used for Timoshenko’s exact solution. As default iteration method is set Picard method . It is suitable for most cases of nonlinear behaviour of buildings and it is set as default for geometrical nonlinearity.
3rd order
It is called “large deformations” which is based on the Newton-Raphson method for the solution of non-linear equations. This method is a more general applicable method which is very solid for most types of problems. It can be used for very large deformations and rotations; however, is also suitable for small displacements and small strains. Mathematically, the method is based on a step-by-step augmentation of the load. This type iterative solution is suitable mostly for models with membranes and cables like for example bridges.
Overview
| Geometrical nonlinearity | Possible methods of calculation |
| 2nd order (Timoshenko) | "Picard_method" |
| 3rd order (large deformation) | " Newton-Raphson method" |
| "Modified Newton Raphson method" | |
| "Picard_method" | |
| "Picard and Newton Raphson" |