Capacity check Theoretical background

 

The capacity check for fibre reinforced concrete is based on the calculation of the resistance of cross-section with the current fibre dosage and standard reinforcement and comparison of it with acting load to get equilibrium of forces.

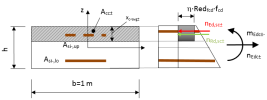
The calculation precognitions for finding plane of equilibrium of steel fibre concrete with reinforcement are taken from Figure R.4 - Determining stresses and strains for steel fibre reinforced concrete from [1] DAfStb Guideline "Steel fibre reinforced concrete".

The following conditions of equilibrium must be fulfilled.

F_c+F_ct+F_s++F_s-+N_Ed =0

F_c. z_c + F_ct.z_ct + F_s+. z_s++F_s-.z_s- + M_Ed =0

Following procedure is used for calculation of the Capacity check for fibre reinforced concrete.

• Definition of the input values for calculation
• The calculation of the height of the compression zone
  • Calculation of the reinforcement material parameters
  • Calculation of the concrete material parameters
  • Calculation of the area of reinforcement
  • Calculation of the diameter of reinforcement
  • Calculation of the cover of reinforcement
  • Calculation of the lever arm of forces in reinforcement from the centre of gravity
  • Calculation of the effective depth of the cross-section
  • Calculation of the centre to centre distance from more compressive edge
  • Calculation of the balanced parameters of the cross-section
  • Calculation of the fibre concrete material parameters in tension
  • Estimation of the reinforcement stress for calculation of the compression zone
  • Calculation of the balanced normal force
  • Calculation of the height of the compression zone
• The calculation of the resistance of the cross-section
  • Calculation of the inner lever arm for concrete and reinforcement from centre of gravity
  • Calculation of the stress in the reinforcement according to height of the compression zone
  • Calculation of the resistance
• Calculation of the unity check

The calculation of the height of the compression zone

Calculation of the reinforcement material parameters

The reinforcement material parameters are calculated independently for upper and lower surface, they can be generally different.

f_yd+(-) = f_yk+(-) / γ_s

E_s+(-)

where

fyk+(-)	Characteristic yield strength of reinforcement, different according Type of calculated reinforcement: Nearest - The strength of reinforcement, which is the nearest to the upper (lower) surface Average - The average strength of all reinforcement which are on upper (lower) surface according to formula fyk+(-) = ∑(As+(-),i ∙ fyk+(-),i) / ∑(As+(-),i) where As+(-),i The area of i-th reinforcement bar on the upper (lower) surface fyk+(-),i Characteristic yield strength of reinforcement of i-th bar on the upper (lower) surface
γs	Partial factor for reinforcing steel, national dependent value in EN 1992-1-1, §2.4.2.4(1), for details see "National annexes theoretical background".
Es+(-)	Modulus of elasticity of reinforcement, different according Type of calculated reinforcement: Nearest - The modulus of elasticity of reinforcement, which is the nearest to the upper (lower) surface Average - The average modulus of elasticity of all reinforcement which are on upper (lower) surface according to formula Es+(-) = ∑(As+(-),i ∙ E+(-),i) / ∑(As+(-),i) where As+(-),i The area of i-th reinforcement bar on the upper (lower) surface E+(-),i Modulus of elasticity of reinforcement of i-th bar on the upper (lower) surface

Calculation of the concrete material parameters

Calculation of the design value of compressive concrete strength

f_cd = α_cc ∙ f_ck / γ_C

where

αcc	The coefficient taking account of long term effects on the compressive strength and of unfavourable effects resulting from the way the load is applied, national dependent value in EN 1992-1-1, §3.1.6(1)P, for details see "National annexes theoretical background".
fck	Characteristic compressive cylinder strength of concrete at 28 days
γC	Partial factor for concrete, national dependent value in EN 1992-1-1, §2.4.2.4(1), for details see "National annexes theoretical background".

Calculation of the strains for concrete stress-strain diagram

Proper strains are used according selected type of stress-strain diagram

• Bilinear - ε_c3, ε_cu3
• Parabolic - ε_c2, ε_cu2

Calculation of the extra rotation point

The extra rotation point is used in the calculation

HeightRatio = 1 - (ε_c2(3) / ε_cu2(3))

StrainRatio = (ε_c2(3) / ε_cu2(3)

Calculation of the strength reduction factor for strength of concrete and position of concrete compressive force

For bilinear stress-strain diagram

η = 1 - (ε_c3 / ε_cu3) / 2

β = 1 - (ε_cu3² / 2 - ε_c3² / 6) / (ε_cu3² - ε_cu3 ∙ ε_c3 / 2)

For parabolic stress-strain diagram

η = 1 - {ε_c2 / [(n + 1) ∙ ε_cu2]}

β = 1 - {ε_cu2² / 2 - ε_c2² / [(n + 1) ∙ (n + 2)]} / [ε_cu2² - ε_cu2 ∙ ε_c2 / (n + 1)]

where

εc2(3)	The strain at the reaching the maximum strength for parabolic (bilinear) stress-strain diagram according to Table 3.1 from EN 1992-1-1
εcu2(3)	The ultimate strain for parabolic (bilinear) stress-strain diagram according to Table 3.1 from EN 1992-1-1
n	The exponent for parabolic stress-strain diagram according to Table 3.1 from EN 1992-1-1

Calculation of the area of reinforcement

The area of reinforcement is calculated as the sum of all reinforcement for upper and lower surface on the 2D element

A_s+(-) = ∑A_s+(-),i

Calculation of the diameter of reinforcement

The diameters of reinforcement bars are calculated independently for upper and lower surface, they can be different.

Different procedure is used according Type of calculated reinforcement:

• Nearest - The diameter of reinforcement bar, which is the nearest to the upper (lower) surface, is used as d_s+(-)
• Average - The average diameter of all reinforcement bars which are on upper (lower) surface, is used as d_s+(-)

d_s+(-) = ∑(A_s+(-),i ∙ d_s+(-),i) / ∑(A_s+(-),i)

where

As+(-),i	The area of i-th reinforcement bar on the upper (lower) surface
ds+(-),i	The diameter of reinforcement of i-th bar on the upper (lower) surface

Calculation of the cover of reinforcement

The cover of reinforcement is calculated independently for upper and lower surface, they can be different.

Different procedure is used according Type of calculated reinforcement:

• Nearest - The cover of reinforcement bar, which is the nearest to the lower (-) and upper (+) surface

c_- = 0.5 ∙ h + Y_(z)-

c₊ = 0.5 ∙ h - Y_(z)+

where

h	Thickness of 2D element
Y(z)-	Y-coordinate (vertical) of the reinforcement which is the nearest to the lower surface
Y(z)+	Y-coordinate (vertical) of the reinforcement which is the nearest to the upper surface

• Average - The average diameter of all reinforcement bars which are on lower (upper) surface

c_-(+) = 0.5 ∙ h - z_s-(+)

where

h	Thickness of 2D element
zs-(+)	The lever arm of forces in reinforcement from the centre of gravity

Calculation of the lever arm of forces in reinforcement from the centre of gravity

The lever arms of forces in reinforcement from the centre of gravity are calculated independently for upper and lower surface, they can be different.

Different procedure is used according Type of calculated reinforcement:

• Nearest - The lever arms of forces in reinforcement, which is the nearest to the lower (-) and upper (+) surface

z_s- = -0.5 ∙ h + c_- + 0.5 ∙ d_s-

z_s+ = 0.5 ∙ h - c₊ - 0.5 ∙ d_s+

where

h	Thickness of 2D element
c-(+)	The cover to the lower (upper) reinforcement
ds-(+)	The diameter of lower (upper) reinforcement

• Average - The average diameter of all reinforcement bars which are on upper (lower) surface

z_s+(-) = ∑(A_s+(-),i ∙ z_s+(-),i) / ∑(A_s+(-),i)

where

As+(-),i	The area of i-th reinforcement bar on the upper (lower) surface
zs+(-),i	The Y-coordinate (vertical) of i-th bar of reinforcement on the upper (lower) surface

Calculation of the effective depth of the cross-section

The effective depth of cross-section is calculated from cover and diameter of reinforcement

d = h - c_-(+) - 0.5 ∙ d_s-(+)

where

h	Thickness of 2D element
c-(+)	The cover to the lower (upper) reinforcement
ds-(+)	The diameter of lower (upper) reinforcement

The decision if lower or upper reinforcement characteristics are used is based on the value of bending moment (positive → lower reinforcement, negative → upper reinforcement.

For fibre concrete without longitudinal reinforcement (A_s,sum = 0 mm²) is d = h.

Calculation of the centre to centre distance from more compressive edge

The centre to centre distance from more compressive edge is calculated from cover and diameter of reinforcement

a_s = c_-(+) + 0.5 ∙ d_s-(+)

where

c-(+)	The cover to the lower (upper) reinforcement
ds-(+)	The diameter of lower (upper) reinforcement

The decision if lower or upper reinforcement characteristics are used is based on the value of bending moment (positive → lower reinforcement, negative → upper reinforcement.

For fibre concrete without longitudinal reinforcement (A_s,sum = 0 mm²) is a_s = 0 mm.

Calculation of the balanced parameters of the cross-section

The balanced parameters ξ_bal for balanced depth of compression zone and depth of the compression zones x_bal are calculated as follows

The decision if ε_cu2 or ε_cu3 are used is based on the type of stress-strain diagram (ε_cu2→ parabolic, ε_cu3→ bilinear).

The decision if lower or upper reinforcement characteristics are used is based on the value of bending moment. For more tensile edge: positive → lower reinforcement, negative → upper reinforcement. For less tensile edge: positive → upper reinforcement, negative → lower reinforcement.

• The balanced parameter for more tensile edge when cross-section is in tension

ξ_bal1,t = ε_cu2(3) / [ε_cu2(3) + (f_yd-(+) / E_s-(+))]

• The balanced parameter for more tensile edge when cross-section is in compression

ξ_bal1,c = ε_cu2(3) / [ε_cu2(3) - (f_yd-(+) / E_s-(+))]

• The balanced parameter for less tensile edge when cross-section is in tension

ξ_bal2,t = ε_cu2(3) / [ε_cu2(3) - (f_yd+(-) / E_s+(-))]

• The balanced parameter for less tensile edge when cross-section is in compression

ξ_bal2,c = ε_cu2(3) / [ε_cu2(3) + (f_yd+(-) / E_s+(-))]

The balanced depth of compression zone is than calculated as follows

• For more tensile edge

x_bal1 = ξ_bal1,t(c) ∙ d

• For less tensile edge

x_bal2 = ξ_bal2,t(c) ∙ d

Calculation of the fibre concrete material parameters in tension

The fibre concrete material parameters are calculated according the recommendations from the Entwurf DAfStb Guideline for Steel fibre reinforced concrete.

The design value of tensile concrete strength

For calculation procedure of f^f_ctd,L1 and f^f_ctd,L2 see the chapter "Design values" in "Materials theoretical background".

The balanced depth of compression zone for fibre concrete

ξ^f_bal,t = ε_cu2(3) / (ε_cu2(3) + ε^f_{ct_L2})

where

εfct_L2

The strain in the fibre reinforced concrete at reaching residual tensile strength in the performance class 2

The tensile strain and stress in fibre concrete

The calculation of stress and strain in fibre concrete in divided to two branches according the ratio of x_c / d with ξ^f_bal,t.

• when x_c / d ≥ ξ^f_bal,t

ε^f_ct = ε_cu2(3) ∙ (d - x_c) / x_c

ε^f_cc = ε_cu2(3)

IF f^f_ctd,L2 < f^f_ctd,L1

THEN f^f_ctd = f^f_ctd,L2 + (f^f_ctd,L1 - f^f_ctd,L2) ∙ (ε^f_{ct_L2} - ε^f_ct) / (ε^f_{ct_L2} - ε^f_{ct_L12})

ELSE f^f_ctd = f^f_ctd,L1 + (f^f_ctd,L2 - f^f_ctd,L1) ∙ (ε^f_ct - ε^f_{ct_L12}) / (ε^f_{ct_L2} - ε^f_{ct_L12})

• when x_c / d < ξ^f_bal,t

ε^f_ct = ε^f_{ct_L2}

ε^f_cc = ε^f_{ct_L2} ∙ x_c/ (d - x_c)

where

εfct_L12

The strain in the fibre reinforced concrete at starting descending branch of residual tensile strength in performance class 1

The reduction factor for tensile strength of concrete and position of concrete tensile force

Two support values are calculated

A^f_ct = 0.5 ∙ (ε^f_{ct_L12} - ε^f_{ct_L11} + ε^f_ct) + 0.5 ∙ (f^f_ctd / f^f_ctd,L1) ∙ (ε^f_ct - ε^f_{ct_L12})

S^f_ct = ε^f_{ct_L11}² / 3 + (ε^f_{ct_L12} - ε^f_{ct_L11})² / 2 + [(f^f_ctd,L1 - f^f_ctd) / f^f_ctd,L1] ∙ [(ε^f_ct - ε^f_{ct_L12}) / 2] ∙ [(ε^f_ct - ε^f_{ct_L12}) / 3 + ε^f_{ct_L12}] + (f^f_ctd / f^f_ctd,L1) ∙ (ε^f_ct - ε^f_{ct_L12}) ∙ [(ε^f_ct - ε^f_{ct_L12}) / 2 + ε^f_{ct_L12}]

The reduction factors are than calculated as follows

η^f_t = A^f_ct / ε^f_ct

β^f_t = S^f_ct / (A^f_ct / ε^f_ct)

λ^f_t = 1.0

Estimation of the reinforcement stress for calculation of the compression zone

Stress in upper and lower reinforcement is estimated for the calculation of first iteration as "starting point". The stresses are generally set to yield strength of reinforcement.

• For only compression load

IF m_Ed = 0

THEN σ_s+(-) = max(-ε_c2(3) ∙ E_s+(-); -f_yd+(-))

ELSE σ_s+(-) = -f_yd+(-)

• For only tension load

σ_s+(-) = -f_yd+(-)

• For compression and tension load together

IF m_Ed ≥ 0

THEN σ_s+ = -f_yd+ and σ_s- = f_yd-

ELSE σ_s+ = f_yd+ and σ_s- = -f_yd-

Calculation of the balanced normal force

The balanced normal force n_Rd,bal is force in the cross-section, when balanced state is adjusted.

n_Rd,bal = - x_bal1 ∙ λ ∙ b ∙ η ∙ f_cd + (h - x_bal1) ∙ λ^f_t ∙b ∙ η^f_t ∙ f_ctd,L1 + A_s+ ∙ σ_s+ + A_s- ∙ f_yd-

Calculation of the height of compression zone

Three possibilities for calculation of the height of compression zone are available

• n_Rd method (height of compression from force)

x_c = (-n_Ed + λ^f_t ∙ b ∙ h ∙ η^f_t ∙ f_ctd,L1 + A_s- ∙ σ_s- + A_s+ ∙ σ_s+) / (λ ∙ b ∙ η ∙ f_cd + λ^f_t ∙ b ∙ η^f_t ∙ f_ctd,L1)

• m_Rd method (height of compression from moment)

β_tin = 1 - β^f_t

A = λ ∙ b ∙ η ∙ f_cd ∙ β + λ^f_t ∙ b ∙ η^f_t ∙ f_ctd,L1 ∙ β_tin

B = -λ ∙ b ∙ η ∙ f_cd ∙ 0,5 ∙ h - λ^f_t ∙ b ∙ η^f_t ∙ f_ctd,L1 ∙ h ∙ (2 ∙ β_tin - 0,5)

C = |m_Ed| + A_s- ∙ σ_s- ∙ z_s- + A_s+ ∙ σ_s+ ∙ z_s+ - λ^f_t ∙ b ∙ η^f_t ∙f_ctd,L1 ∙ h² ∙ (0,5 - β_tin)

D = B² - 4 ∙ A ∙ C

if D ≥ 0

THEN x_c = (-B - √D) / (2 ∙ A)

ELSE x_c = -999 and error message is shown

• n_Rd/m_Rd method (height of compression from eccentricity)

eccentricity: e = -|m_Ed / n_Ed|

β_tin = 1 - β^f_t

A = λ ∙ b ∙ η ∙ f_cd ∙ β + λ^f_t ∙ b ∙ η^f_t ∙ f_ctd,L1 ∙ β_tin

B = -λ ∙ b ∙ η ∙ f_cd ∙ (0,5 ∙ h - e) - λ^f_t ∙ b ∙ η^f_t ∙ f_ctd,L1 ∙ h ∙ (2 ∙ β_tin - 0,5 ∙ h + e)

C = A_s- ∙ σ_s- ∙ (z_s- - e) + A_s+ ∙ σ_s+ ∙ (z_s+ - e) - λ^f_t ∙ b ∙ η^f_t ∙f_ctd,L1 ∙ h² ∙ (0,5 ∙ h - β_tin ∙ h - e)

D = B² - 4 ∙ A ∙ C

if D ≥ 0

THEN x_c = (-B -(+) √D) / (2 ∙ A) (- when e < 0; + when e > 0)

ELSE x_c = -999 and error message is shown

The calculation of the resistance of the cross-section

Calculation of the inner lever arm for concrete and reinforcement from centre of gravity

Inner level arm of compressive forces in concrete from centre of gravity

IF m_Ed ≥ 0

THEN z_cc = 0,5 ∙ h - β ∙ x_c

ELSE z_cc = -0,5 ∙ h + β ∙ x_c

Inner level arm of tensile forces in concrete from centre of gravity

IF m_Ed ≥ 0

THEN z_ct = - x_c - (h - x_c) ∙ β^f_t + 0,5 ∙ h

ELSE z_ct = + x_c + (h - x_c) ∙ β^f_t - 0,5 ∙ h

IF x_c < 0, THAN z_ct = 0

Calculation of the stress in the reinforcement according to height of the compression zone

Three possible states for recognition of stress in reinforcement, based on comparison of x_c with d and a_s.

• x_c ≤ d and x_c ≥ a_s

IF m_Ed ≥ 0

THEN σ_s+ = -f_yd+; σ_s- = f_yd-

ELSE σ_s+ = f_yd+; σ_s- = -f_yd-

• x_c < a_s

σ_s+ = f_yd+; σ_s- = f_yd-

• x_c > d

IF m_Ed = 0

THEN σ_s+ = max(-ε_c2(3) ∙ E_s+, -f_yd+) ; σ_s- = max(-ε_c2(3) ∙ E_s-, -f_yd-)

ELSE σ_s+ = -f_yd+; σ_s- = -f_yd-

Calculation of the resistance

The resistance of the cross-section is based on calculation of forces in compressive and tensile concrete and in reinforcement and than these forces are multiplicative by inner level arms to obtain final resistances.

• Concrete compressive area

A_cc = x_c ∙ b

• Concrete tensile area

A_ct = (h - x_c) ∙ b

• Minimal concrete stress

σ_cc = -f_cd

• Maximal concrete stress (tension)

σ_ct = f_ctd,L1

• Compressive force in concrete

F_cc = A_cc ∙ η ∙ σ_cc

• Tensile force in concrete

IF x_c > 0

THEN F_ct = A_ct ∙ η^f_t ∙ σ_ct

ELSE F_ct = A_ct ∙ f_ctd,L2

• Forces in lower (-) and upper (+) reinforcement

F_s-(+) = A_s-(+) ∙ σ_s-(+)

• Resistances of the cross-section

n_Rd = F_cc + F_ct + F_s- + F_s+

m_Rd = - F_cc ∙z_cc - F_ct ∙ z_ct - F_s- ∙z_s- - F_s+ ∙ z_s+

The calculation of the unity check

Final unity check is calculated according selected type of method for calculation

• n_Rd method

UC = m_Ed / m_Rd

• m_Rd method

UC = n_Ed / n_Rd

• n_Rd/m_Rd method

UC = max(m_Ed / m_Rd, n_Ed / n_Rd, (n_Ed² + m_Ed²)^0,5 / (n_Rd² + m_Rd²)^0,5)

Final value of unity check can be drawn in 3D scene in SCIA Engineer.

Check of the compression strut

On addition to capacity check is the check of compression strut. The internal forces which are calculated in the direction of the concrete strut have to be also checked. The internal forces have to be carried by concrete in compression.

The depth of the compression zone is calculated for each surface as average values from user defined reinforcement for both directions

x_c,avg± = 0,5 ∙ (x_c,1± + x_c,2±)

where

xc,1±	Depth of the compression zone calculated from user defined reinforcement in the first direction
xc,2±	Depth of the compression zone calculated from user defined reinforcement in the second direction

Design value of resistance of concrete compressive strut is calculated according formula

n_Rd,sc± = -A_cc± ∙ η ∙ Red_fcd ∙ f_cd

where

Acc±	The area of the compression concrete at upper (lower) surface Acc± = xc,avg± ∙ 1 m
η	The coefficient for reduction design compressive strength of the concrete from concrete setup
Redfcd	The coefficient for reduction strength of the concrete in compressive concrete strut from concrete setup
fcd	The design compressive strength of concrete

Unity check is than calculated as follows

UC_sc = max(n_Ed,sc+ / n_Rd,sc+, n_Ed,sc- / n_Rd,sc-)

The value of Unity check for compression strut is also part of capacity check UC

UC = max(UC_capacity, UC_sc)