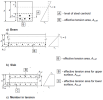
Crack width theoretical background

 

The crack width for slabs with standard reinforcement

When standard reinforcement exists, the crack width is calculated according equation R.7.8 [1] DAfStb Guideline "Steel fibre reinforced concrete":

w_k = s_r,max ∙ (ε^f_sm - ε_cm)

where

sr,max	The maximum final crack spacing.
(εfsm - εcm)	The difference between mean strains in concrete and reinforcement in case of steel fibre reinforced concrete.

The maximum final crack spacing

s_r,max = (1 - α_f) ∙ ϕ_s / (3,6 ∙ ρ_p,eff) ≤ (1 - α_f) ∙ (σ_s ∙ ϕ_s) / (3,6 ∙ f_ct,eff)

where

αf	The coefficient for fibre reinforcement concrete αf = ffctR,s / fctm
ϕs	Averaged diameter of reinforcement, see the chapter Calculation of the diameter of reinforcement in "Capacity check theoretical background"
ρp,eff	The effective reinforcement ratio obtained from the equation 7.10 from [2] EN1992-1-1 ρp,eff = As / Ac,eff
fct,eff	The effective tensile strength of concrete

The difference between mean strains

The difference is calculated according equation R.7.9

(ε^f_sm - ε_cm) = ((1 - α_f) ∙ (σ_s - 0,4 ∙ f_ct,eff / ρ_p,eff)) / E_s ≥ 0,6 ∙ (1 - α_f) ∙ σ_s / E_s

where

αf	The coefficient for fibre reinforcement concrete αf = ffctR,s / fctm
ϕs	Averaged diameter of reinforcement, see the chapter Calculation of the diameter of reinforcement in "Capacity check theoretical background"
ρp,eff	The effective reinforcement ratio obtained from the equation 7.10 from [2] EN1992-1-1 ρp,eff = As / Ac,eff where As The area of reinforcement inside of Ac,eff Ac,eff The effective concrete area see figure 7.1 in [2] EN1992-1-1
fct,eff	The effective tensile strength of concrete
εfsm	The mean strain in the reinforcement in steel fibre reinforced concrete for the relevant combination of actions taking tension stiffening into account
εcm	The mean strain in concrete between cracks
σs	The reinforcement stress in the crack without taking into account the fibre effect. Maximal value of tensile stress of the reinforcement inside area Ac,eff.
Es	Modulus of elasticity of standard reinforcement

The crack width for slabs without standard reinforcement

When standard reinforcement does not exists on selected 2D member, the crack width is calculated according equation R.7.11 [1] DAfStb Guideline "Steel fibre reinforced concrete":

w_k = s^f_w ∙ ε^f_ct

where

sfw	= 140 mm
εfct	The strain in the steel fibre reinforced concrete, where stress-strain diagram is same as for standard concrete with linear effective branch in tension

Recalculation of internal forces and reinforcement areas for Crack width

The crack width are calculated in the direction of principal forces. Therefore is necessary to recalculate basic internal forces and the reinforcement areas to the principal directions.

Normal stresses per directions and surfaces

Normal stresses per each direction of member LCS and for upper(lower) surface are calculated.

σ_x,up(lo) = n_x / (h ∙ 1m) -(+) m_x / (1/6 ∙ h² ∙ 1m)

σ_y,up(lo) = n_y / (h ∙ 1m) -(+) m_y / (1/6 ∙ h² ∙ 1m)

σ_xy,up(lo) = n_xy / (h ∙ 1m) -(+) m_xy / (1/6 ∙ h² ∙ 1m)

where

nx(y)	Normal force in centre of mesh element in x(y) direction
mx(y)	Bending moment in centre of the mesh element in x(y) direction
nxy	Membrane shear force in centre of the mesh element
mxy	Twisting moment in centre of the mesh element
h	Thickness of the 2D member

Principal stresses for both surfaces

σ_1,up(lo) = (σ_x,up(lo) + σ_y,up(lo)) / 2 + 1/2 ∙ √(σ_x,up(lo) - σ_y,up(lo))² + 4 ∙ σ_xy,up(lo)²)

σ_2,up(lo) = (σ_x,up(lo) + σ_y,up(lo)) / 2 - 1/2 ∙ √(σ_x,up(lo) - σ_y,up(lo))² + 4 ∙ σ_xy,up(lo)²)

and σ_1,up(lo) is greater than σ_2,up(lo)

Angles of principal stresses from y axis for both surfaces

First direction

when (σ_x,up(lo) - σ_y,up(lo)) > 0

α_σ1,up(lo) = arctg(2 ∙ σ_xy,up(lo) / (σ_x,up(lo) - σ_y,up(lo))) / 2

when (σ_x,up(lo) - σ_y,up(lo)) < 0

α_σ1,up(lo) = arctg(2 ∙ σ_xy,up(lo) / (σ_x,up(lo) - σ_y,up(lo))) / 2 - 90 °

when (σ_x,up(lo) - σ_y,up(lo)) = 0

• when σ_xy,up(lo) = 0

α_σ1,up(lo) = 0

• when σ_xy,up(lo) < 0

α_σ1,up(lo) = -45 °

• when σ_xy,up(lo) > 0

α_σ1,up(lo) = 45 °

Second direction

α_σ2,up(lo) = α_σ2,up(lo) + 90 °

Recalculation of areas of reinforcement to direction of principal stresses

When standard reinforcement 2D mesh is defined, than is necessary to recalculate its area to the direction of principal stress.

A_s(α_σ) = ∑(A_s,i ∙ cos(α_σ - α_s,i))

where

As,i	The area of the i-th reinforcement layer in the mesh element
ασ	Angle between y-axis and the direction of the principal stress for first or second direction
αs,i	Angle between y-axis and the direction of the i-th reinforcement layer

Recalculation of the internal forces for the crack width

m_up(lo) = m_x ∙ cos(α_σ,up(lo))² + m_y ∙ sin(α_σ,up(lo))² + m_xy ∙ sin(2 ∙ α_σ,up(lo))

n_up(lo) = n_x ∙ cos(α_σ,up(lo))² + n_y ∙ sin(α_σ,up(lo))² + n_xy ∙ sin(2 ∙ α_σ,up(lo))

The recalculation is done four times in total. Once per direction and surface.

Limit value of crack width

When steel fibre reinforcement concrete contains standard reinforcement 2D meshes, than is the limit value of crack width w_lim taken same as for standard concrete according clause 7.3.1(5) from [2] EN1992-1-1

When steel fibre reinforcement concrete does not contain standard reinforcement, than is the limit value of crack width w_lim taken from the National annex manager in group SLS - General. Where is new item - w_{max_fibre} according the [1] DAfStb Guideline "Steel fibre reinforced concrete"in table R.4.