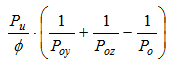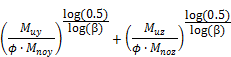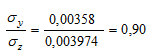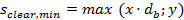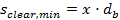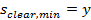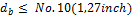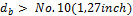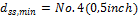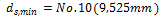8.2 Design of reinforcement for 1D members (beams, beams as slab, columns)
There is different procedure for design of longitudinal and shear reinforcement for beams, beams as slab and for columns.
8.2.1 Beams and beams as slab – design of reinforcement
8.2.1.1 Method for calculation strength reduction factor
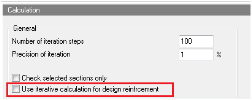
There are three basic methods for design of longitudinal reinforcement. The decision which method will be used depends on the setting in concrete setup and in concrete member data. There are new options Use iterative calculation for design reinforcement in Concrete setup>General >Calculation and Type of strength reduction factor in concrete member data.
The three methods are the following:
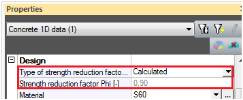
Method 1 (User input value of Phi) – Use iterative calculation for design reinforcement is not important for this method and concrete member data is defined and Strength reduction factor Phi = User input
Method 2 (Iterative calculation value Phi) – Use iterative calculation for design reinforcement is ON and concrete member data is not defined or concrete member data is defined but Strength reduction factor Phi = Calculated
Method 3 (Non-iterative calculation value Phi) – Use iterative calculation for design reinforcement is OFF and concrete member data is not defined or concrete member data is defined but Strength reduction factor Phi = Calculated
| Method | Use iterative calculation for design reinforcement | Concrete member data defined | Strength reduction factor |
|---|---|---|---|
| Method 1 | Not important | YES | User input |
| Method 2 | ON | YES or NO | Calculated |
| Method 3 | OFF | YES or NO | Calculated |
8.2.1.1.1 Method 1 (User input value of Phi)
This method is used when Strength reduction factor Phi = User input in concrete member data
Strength reduction factor is loaded from concrete member data (User input value)
Calculation of nominal values of internal forces
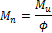
and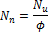
Design reinforcement for normal force Nn and bending moment Mn
8.2.1.1.2 Method 2 (Iterative calculation value Phi)
The iterative method is used for calculation of strength reduction factor (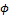 ). The procedure of this method is the following:
). The procedure of this method is the following:
Estimation of strength factor: 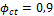 (the value is input in Concrete setup for tension –Controlled section); strain in reinforcement steel has to be
(the value is input in Concrete setup for tension –Controlled section); strain in reinforcement steel has to be 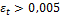
Calculation of nominal values of internal forces
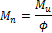
and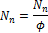
Design reinforcement for normal force Nn and bending moment Mn
Check of tensile strain in reinforcement:
IF( 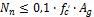 ) or (
) or (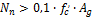 and check box Check compression of element is OFF) then:
and check box Check compression of element is OFF) then:
Else status of calculation is NOT OK and finishes with error (E915 - Member in compression, should be design as column)
8.2.1.1.3 Method 3 (Non-iterative calculation value Phi)
The design reinforcement without iteration run according to following procedure:
Estimation of strength factor: 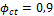 (the value is input in Concrete setup for tension –Controlled section); strain in reinforcement steel has to be
(the value is input in Concrete setup for tension –Controlled section); strain in reinforcement steel has to be 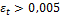
Calculation of nominal values of internal forces
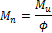
and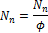
Design reinforcement for normal force Nn and bending moment Mn
Check of tensile strain in reinforcement:
IF( 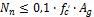 ) or (
) or (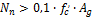 and check box Check compression of element is OFF) then:
and check box Check compression of element is OFF) then:
|
Strain |
Estimation |
|---|---|
|
|
Estimation of strength reduction factor is OK |
|
|
Estimation is OK BUT calculation finishes with warning (W301 - The section is in transition zone, but strength reduction factor for tension-controlled section is used)
|
|
|
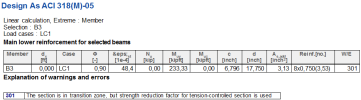
Estimation is NOT OK and calculation is finished with error (E916 - the cross-section is not ductile) |
Value  is value equal to 0,004 (see chapter 4.1.4.3 Maximum strain for non-prestressed flexural member)
is value equal to 0,004 (see chapter 4.1.4.3 Maximum strain for non-prestressed flexural member)
Else status of calculation is NOT OK and finishes with error (E915 - Member in compression, should be design as column)
- calculation cbal = εcu⋅d/(εcu + fy/Es)
Output with W301
Output with E916
Explanation of values printed in the preview
|
Value |
Description |
|---|---|
|
Member |
Name of the checked member |
|
dx |
Position of the checked section on member |
|
Case |
|
|
f |
Strength reduction factor |
|
εst |
Calculated strain in reinforcement |
|
Nu |
Factored normal force |
|
Muy |
Factored bending moment around y axis |
|
Muz |
Factored bending moment around z axis |
|
c |
Depth of the compression zone |
|
d |
Effective depth |
|
As,add |
Area of additional longitudinal reinforcement |
|
W/E |
Warning and errors |
8.2.1.2 Longitudinal reinforcement
There is only one difference between design of reinforcement for “Beam” and “Beam as slab”. The shear reinforcement is not designed for member type “beam as slab”. The design of longitudinal reinforcement is the same for “beam” and “beam slab” too.
When shear reinforcement is designed for member type “beam slab” then special warning appears (W90 – No shear reinforcement calculated, since the beam is considered to be floor without shear reinforcement)
The procedure of design of longitudinal reinforcement is based on the calculation of equilibrium between internal forces and external load. This is general method independent on the used method.
There are the following preconditions:
Parabola-rectangle strain-stress diagram for concrete
Bilinear strain-stress diagram for reinforcement
8.2.1.2.1 Design of compressive reinforcement
The different procedure is used when it is necessary to design also compressive reinforcement. This procedure is applied when:
the tensile reinforcement is not enough sufficient (ductility check is NOT OK)
checkbox Design compression reinforcement is switch ON then the following is done:
area of compression reinforcement is 0inch2
Then design of reinforcement is provided as the following:
maximum tensile strain in steel is εt = 0,005
new maximal depth of compression zone is calculated based on maximum tensile strain
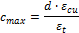
8.2.1.2.2 Maximum reinforcement factor (chapter 10.3.5 from ACI 318-05)
When user switches ON this checkbox then the strain in reinforcement has to be higher than inputted value 0,004=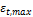 . Otherwise the section is not ductile.
. Otherwise the section is not ductile.
8.2.1.2.3 Detailing provisions
Detailing provisions for beams are verified. These detailing provisions are done for longitudinal and shear reinforcement separately.
8.2.1.2.3.1 Minimum reinforcement factor (chapter 10.5.1 from ACI 318-05)
When the designed are of reinforcement is too low then minimum are of reinforcement has to be used. Settings for this verification are explained in chapter "4 Global setting ". If the first two checkboxes are switch ON then calculation logic is the following
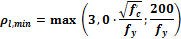
The existence of the tensile zone is checked.
- IF tensile zone exists THEN reinforcement is designed for the tensile fibre using whole reinforcement factor (W148)
- IF tensile zone doesn’t exist THEN reinforcement is designed for each surface using half value of the reinforcement factor and using effective depth related to the bottom fibres (W2)
8.2.1.2.3.2 Minimal clear distance between bars (chapter 7.6.1 from ACI 318-05)
When user switches ON the checkboxes related to minimal clear distance between bars then this detailing provision is verified during the design procedure.
Minimal clear distance between bars is set as
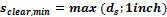
8.2.1.2.3.3 Maximal clear distance between bars (chapter 10.6.4 from ACI 318-05)
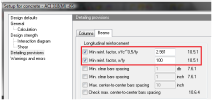
Maximal clear distance between bars is also checked. There are two items related to maximal clear distance between bars (see chapter "4 Global setting "). Maximal allowed centre to centre bars spacing between longitudinal bars is based on the chapter 10.6.4 from ACI 318-05 and on user defined value

Where
fs – stress in reinforcement closest to the tension face; can be taken as 2/3 fy
cc – the least distance from the surface of the bar to the tensile surface of cross-section
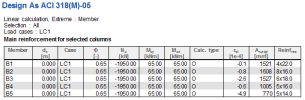
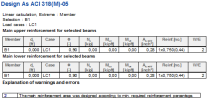
8.2.1.2.4 Table in document for member check
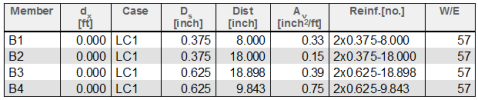
Main upper/lower reinforcement for selected beams
|
Member |
dx |
Case |
φ |
Nu |
Mu |
c |
d |
As,add |
Reinf. |
W/E |
|---|---|---|---|---|---|---|---|---|---|---|
|
|
[m] |
|
|
[kN] |
[kNm] |
[mm] |
[mm] |
[mm2] |
|
|
|
Explanation of symbol |
|
|
f |
Strength reduction factor |
|
Nu |
Factored axial normal force |
|
Mu |
Factored bending moment |
|
c |
Distance from extreme compression fibre to neutral axis |
|
d |
Distance from extreme compression fibre to centroid of longitudinal tension reinf. |
|
As,add |
Theoretical reinforcement area |
|
|
|
|
Table composer |
|
|
εc |
Max. compression strain in concrete |
|
εsc |
Max. compression strain in reinforcement |
|
εst |
Max. tension strain in reinforcement |
|
σc |
Max. compression stress in concrete |
|
σsc |
Max. compression stress in reinforcement |
|
σst |
Max. tension stress in reinforcement |
|
db |
Nominal diameter of longitudinal bar |
|
#bars |
Number of needed bars |
|
As,user |
User defined reinforcement area |
|
As,perc |
Percentage of reinforcement in upper/lower zone |
|
cbal |
Distance from extreme compression fibre to neutral axis for balanced strain conditions |
8.2.1.3 Shear reinforcement
General principles for design is the following:
- The maximum value fy used in calculation is fy = min (fy; fy_shear)
- Only stirrups perpendicular to axis of member are supported
Only concrete with value fc’ > fc_min can be used for design (value fc_min is defined in Concrete setup> General >Concrete)
Concrete with value fc’ < fc_max can be used for design (value fc_max is defined in Concrete setup> General >Concrete), if check box “Check min. area Av.min = x*bw*s/fyt”(Concrete setup >Detailing provisions >Beams > Shear reinforcement) is turned off
Design procedure:
- Strength factor for shear: φ = 0,75 (the value is input in Concrete setup for tension – controlled section)
- Calculation of shear strength provided by concrete Vc is done according to chapter 11.3.2. The way of calculation is dependent on type of dominant load. The basic shear capacity of concrete is the following (formula 11-5)
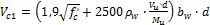
- Tension
- Calculation Vct1 (formula 11-8)
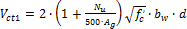
- Calculation Vct,max (limit from formula 11-5)
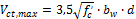
- Calculation of resultant shear capacity of concrete for tension memebr

- Compression
- Calculation Vcc1 (formulas 11-5+11.6)
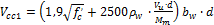
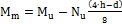
- Calculation Vcc,max (limit from formula 11-7)
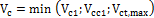
- Calculation strength provided by shear reinforcement (formula 11-2)
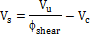
- Calculation of maximal capacity in reinforcement (11.5.7.9.) and performing additional check Vs<Vs,max
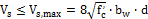
- Calculation of required area of shear reinforcement Asv according to formula (11-15)
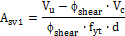
- Based on the minimum required reinforcement (chapter 11.5.6) where
Vu ≥ 0,5 Vc
Vc
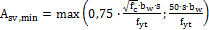
s – user defined value in concrete member data
- Based on the spacing of shear reinforcement
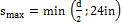
In case Vs ≥ Vs,max/2
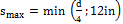
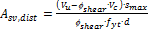
- Resultant area of shear reinforcement is
-
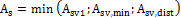
- Calculation of real distance between stirrup
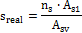
8.2.1.3.1 Detailing provisions
Check detailing provisions for beams and shear reinforcement
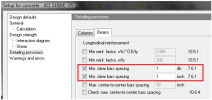
8.2.1.3.1.1 Maximal centre to centre spacing of stirrups legs (chapter 11.5.5 from "10 Literature")
Maximal centre to centre spacing of stirrups legs is checked if the checkbox in concrete setup is switched ON. There are two different values dependent on shear reinforcement resistance of and maximal shear capacity of cross-section
|
Unit format |
Formula |
spacing |
|---|---|---|
|
US |
|
|
|
|
|
|
|
Metric |
|
|
|
|
|
|
Where values mean
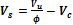 – shear reinforcement resistance of concrete section
– shear reinforcement resistance of concrete section
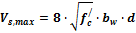 - maximal shear resistance of concrete section
- maximal shear resistance of concrete section
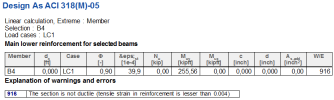
When reinforcement is designed according to this provision then warning appears (W52 - The shear reinforcement was designed according to code longitudinal distance of stirrups).
8.2.1.3.1.2 Minimal percentage of shear reinforcement (chapter 11.5.6 from "10 Literature")
Minimal percentage of shear reinforcement is checked if the checkbox in concrete setup is switched ON. There are two different values dependent on shear resistance of cross-section and maximal shear capacity
|
Unit format |
Formula |
spacing |
|---|---|---|
|
US |
|
|
|
|
|
|
|
Metric |
|
|
|
|
|
|
Where values mean
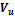 – factored shear force acting on structure
– factored shear force acting on structure
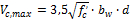 - maximal shear resistance of concrete section
- maximal shear resistance of concrete section
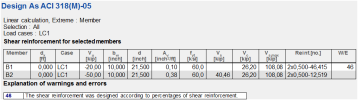
When reinforcement is designed according to this provision then warning appears (W46 - The shear reinforcement was designed according to percentage of shear reinforcement).
8.2.1.3.1.3 Minimal diameter of shear reinforcement
Minimal allowed diameter of shear reinforcement is checked if the checkbox in concrete setup is switched ON. This check depends on defined diameter of longitudinal reinforcement in concrete member data and diameter of stirrup.
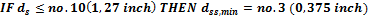
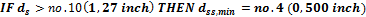
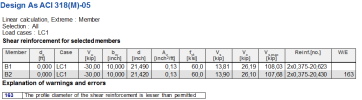
When lesser diameter of shear reinforcement is defined in concrete member data then warning appears. (W163 – The profile of the shear reinforcement is lesser than permitted)
8.2.1.3.1.4 Maximal transverse spacing of the legs
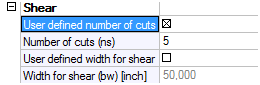
Maximal transverse spacing of the legs is checked if the checkbox in concrete setup is switched ON. This value is code independent and it is user value. Default is 12 inch. The check is performed in Concrete member data. When the checkbox user defined number of cuts is set ON then maximal transverse spacing of the stirrups legs is checked.
Minimal number of cuts is calculated based on this distance and user is not allowed to input less value then calculated by program. Otherwise the following message appears.
Shear reinforcement for selected members
|
Member |
dx |
Case |
φ |
Vu |
bw |
d |
Vc |
Av |
Reinf. |
W/E |
|---|---|---|---|---|---|---|---|---|---|---|
|
|
[m] |
|
|
[kN] |
[mm] |
[mm] |
[kN] |
[mm2] |
|
|
|
Explanation of symbol |
|
|
f |
Strength reduction factor for shear |
|
Vu |
Factored shear force |
|
bw |
Width of section for shear |
|
d |
Distance from extreme compression fiber to centroid of longitudinal tension reinf. |
|
Vc |
Nominal shear strength provided by concrete |
|
Av |
Area of shear reinforcement |
|
|
|
|
Table composer |
|
|
Nu |
Factored axial normal force |
|
Mu |
Factored bending moment |
|
Mm |
Factored moment modified to account for effect of axial compression |
|
Vs |
Nominal shear strength provided by shear reinforcement |
|
Vs.max |
Maximal nominal shear strength provided by shear reinforcement |
|
Av,min |
Minimum area of shear reinforcement |
|
ds |
Nominal diameter of shear reinforcement |
|
s |
Centre to centre spacing of shear reinforcement |
|
fyt |
Specified yield strength of shear reinforcement |
8.2.2 Column – design of reinforcement
8.2.2.1 Method for calculation strength reduction factor
There are three basic methods for design of longitudinal reinforcement. The decision which method will be used depends on the setting in concrete setup and in concrete member data. There are new options Use iterative calculation for design reinforcement in Concrete setup > General > Calculation, see chapter "4.1 Concrete setup for 1D member" and Type of strength reduction factor in concrete member data, see chapter "5.2 Member data 1D (beams, beams as slab, columns)".
|
Concrete setup >General > Calculation |
Concrete member data |
|---|---|
The three methods are the following:
Method 1 (User input value of Phi) – check box Use iterative calculation for design reinforcement is not taken into account for this method and concrete member data has to be defined and Type of strength reduction factor = User input
Method 2 (Iterative calculation value Phi) – check box Use iterative calculation for design reinforcement is ON and concrete member data is not defined or concrete member data is defined and Type of strength reduction factor Phi = Calculated
Method 3 (Non-iterative calculation value Phi) – check box Use iterative calculation for design reinforcement is OFF and concrete member data is not defined or concrete member data is defined and Type of strength reduction factor Phi = Calculated
| Method |
Use iterative calculation for design reinforcement |
Concrete member data defined |
Type of strength reduction factor |
|---|---|---|---|
|
Method 1 |
- |
YES |
User input |
|
Method 2 |
ON |
YES or NO |
Calculated |
|
Method 3 |
OFF |
YES or NO |
Calculated |
8.2.2.1.1 Method 1 (User input value of φ)
This method is used when Strength reduction factor Phi = User input in concrete member data. The following procedure is used:
For all section in the member the same value of strength reduction factor is used
Strength reduction factor φ is loaded from concrete member data (User input value)
Design reinforcement for normal force Pu/φ and bending moments Muy/φ and Muz/φ according to selected method, see chapter "8.2 Design of reinforcement for 1D members (beams, beams as slab, columns)"
The value of strain on the most tensioned reinforcement is not checked.
8.2.2.1.2 Method 2 (Iterative calculation value φ)
This method is used, if check box Use iterative calculation for design reinforcement is ON and concrete member data is not defined or concrete member data is defined and Type of strength reduction factor Phi = Calculated. The iterative calculation for calculation strength reduction factor is used, it mean that the calculation takes longer time, but the results are more precise. The value φ are calculated from values defined in concrete setup depending on strain in mots-tensioned reinforcement (value εt) and on axial force. It follows, that for each section of the member different value strength reduction factor can be used. The following procedure is used:
For tensile axial force and pure bending (Pu ³ 0)
- The strength reduction factored is estimated. The strength reduction factor for tension controlled section (φ=φtc) defined in concrete setup is taken into account as default, see chapter 4.1.4.5.2 Tension controlled section
- design reinforcement for axial force Pu/φ and bending moments Muy/φ and Muz/φ according to selected method, see chapter "8.2 Design of reinforcement for 1D members (beams, beams as slab, columns)".
- The strain in the most tensioned reinforcement is checked
|
Strain |
Calculation and result of calculation |
|---|---|
|
|
Estimation of strength reduction factor is OK and calculation is OK |
|
|
Estimation is NOT OK and iterative calculation is used
Iteration will be finished if strain in most tensioned reinforcement in two consecutive steps is lesser than precision of calculation
|
|
|
Estimation is NOT OK and new value of strength reduction factor will be used (the value for compression controlled section φ=φcc )
|
For compressive axial force (Pu < 0)
- The strength reduction factored is estimated. The strength reduction factor for compression controlled section (φ=φcc) defined in concrete setup is taken into account as default, see chapter 4.1.4.5.1 Compression controlled section
- design reinforcement for axial force Pu/φ and bending moments Muy/φ and Muz/φ according to selected method, see chapter "8.2 Design of reinforcement for 1D members (beams, beams as slab, columns)".
- The strain in the most tensioned reinforcement is checked
|
Strain |
Calculation and result of calculation |
|---|---|
|
|
Estimation of strength reduction factor NOT OK and new value of strength reduction factor will be used (the value for tension- controlled section φ=φtc)
|
|
|
Estimation is NOT OK and iterative calculation is used
Iteration will be finished if strain in most tensioned reinforcement in two consecutive steps is lesser than precision of calculation |
|
|
Estimation of strength reduction factor is OK and calculation is OK |
|
where |
|
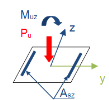
|
Pu |
Axial factored force |
|
Muy(z) |
factored bending moment about y (z) axis of LCS. If magnified moments have to be taken into account, then Muy(z) =Muy(z),rec |
|
Muy(z),rec |
Recalculated factored bending moment with slenderness effect (magnified moments), see chapter "7.2 Internal forces for 1D members (beam, beam as slab, column)" |
For strain in most tensioned reinforcement in cross-section is SEN is used symbol εst instead of value εt
8.2.2.1.3 Method 3 (Non-iterative calculation value φ)
This method is used check box Use iterative calculation for design reinforcement is ON and concrete member data is not defined or concrete member data is defined and Type of strength reduction factor Phi = Calculated. The value φ are loaded from concrete setup depending on value of axial force (Pu) in section. It follows, that for each section of the member different value strength reduction factor can be used. The following procedure is used:
For tensile axial force and pure bending (Pu³ 0)
- The strength reduction factor for tension controlled section (φ=φtc) defined in concrete setup is taken into account, see chapter 4.1.4.5.2 Tension controlled section
- design reinforcement for axial force Pu/φ and bending moments Muy/φ and Muz/φ according to selected method, see chapter "8.2 Design of reinforcement for 1D members (beams, beams as slab, columns)".
- The strain in the most tensioned reinforcement is checked
|
Strain |
Result of calculation |
|---|---|
|
|
The strength reduction factor is correct and calculation is OK |
|
|
The strength reduction factor is incorrect and calculation finishes with warning 301 (The section is in transition zone, but strength reduction factor for tension-controlled section is used) |
|
|
The strength reduction factor is incorrect and calculation finishes with warning 302 (The section is compression-controlled, but strength reduction factor for tension-controlled section is used) |
For compressive axial force (Pu < 0)
- The strength reduction factor for compression controlled section (φ=φcc) defined in concrete setup is taken into account, see chapter 4.1.4.5.1 Compression controlled section
- design reinforcement for axial force Pu/φ and bending moments Muy/φ and Muz/φ according to selected method, see chapter "8.2 Design of reinforcement for 1D members (beams, beams as slab, columns)".
- The strain in the most tensioned reinforcement is checked
|
Strain |
Result of calculation |
|---|---|
|
|
The strength reduction factor is incorrect and calculation finishes with warning 303 (The section is tension-controlled , but strength reduction factor for compression-controlled section is used) |
|
|
The strength reduction factor is incorrect and calculation finishes with warning 301 (The section is in transition zone, but strength reduction factor for tension-controlled section is used) |
|
|
The strength reduction factor is correct and calculation is OK |
|
where |
|
|
Pu |
Axial factored force |
|
Muy(z) |
factored bending moment about y (z) axis of LCS. If magnified moments have to be taken into account, then Muy(z) =Muy(z),rec |
|
Muy(z),rec |
Recalculated factored bending moment with slenderness effect (magnified moments), see chapter 7.2.2 Column |
For strain in most tensioned reinforcement in cross-section is SEN is used symbol εst instead of value εt
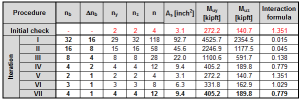
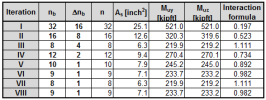
In the table below are compared results of design reinforcement with using Method 2 (iterative calculation of value φ) and Method 3 (non-iterative calculation of value φ) for column with different values internal forces.
|
Method 2 |
|
|
Method 3 |
8.2.2.2 Longitudinal reinforcement
The design of longitudinal reinforcement depends on method for calculation strength reduction factor and on method for design reinforcement in the main. For detailed procedure of calculation strength reduction factor see chapter "8.2 Design of reinforcement for 1D members (beams, beams as slab, columns)"
8.2.2.2.1 Method for design of reinforcement for column
There is supported following methods and cross-sections for design longitudinal reinforcement for column:
|
Method |
Mark |
Supported cross-section |
|---|---|---|
|
Only corner design |
C |
Rectangular, T, I, L sections |
|
Uniaxial bending calculation (sum) |
Us |
Rectangular cross-section |
|
Uniaxial bending calculation (max) |
Um |
Rectangular cross-section |
|
Biaxial bending calculation |
B |
Rectangular cross-section |
|
Design for circular column |
C |
Circular cross-section |
|
Automatic calculation |
B or Um |
Rectangular cross-section |
If compression member (column) is loaded only by axial force (bending moment about y and z axis of compression member are zero), then reinforcement is designed only for this axial load and method of calculation is N/A
Five methods of design reinforcement is supported for rectangular column, therefore it is very important select the correct method of calculation depending on values of bending moments or used automatic calculation. In the table below are compared results of design reinforcement for rectangular columns for different method (B1-only corner design, B2- Uniaxial bending calculation (sum), B3 - Uniaxial bending calculation (max) , B4 – biaxial bending calculation, B5- automatic calculation )
The following preconditions are used for all methods:
- The longitudinal reinforcement is designed for factored internal forces divided by strength reduction factor (Pu/φ ,Muy/φ and Muz/φ).
- For all methods design axial strength φ·Pn of compression members shall not be taken greater than φ·Pn,max,computed according to ACI 318-05,clause 10.3.6.1, see chapter
- the position bars in is calculated from parameters defined in concrete setup ( item Design default > Column, see chapter 4.1.1 Design default), if concrete member data is not defined or from concrete member data (group Design, see chapter "5.2 Member data 1D (beams, beams as slab, columns)" ) otherwise. The following parameters are used for calculation of position:
- concrete cover c
- diameter of stirrup ds
- diameter of longitudinal reinforcement d
|
Member without concrete member data |
Member with concrete member data |
The results of design longitudinal reinforcement are presented in numerical and graphical output and detailed results for each section can be presented via action button Single check
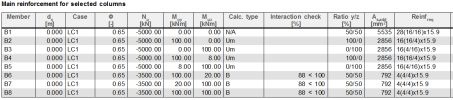
The numerical output is available after clicking on action button Preview. The numerical output does depend on selected value. The table of longitudinal reinforcement is presented, if values As,total, req; As user define; As add,req is presented
There is available more detailed tables for columns (for example table with detailed presentation of area of reinforcement, or table with detailed presentation of number of bars ). These detailed tables can be selected after clicking on the header of the table and by selecting the type of the table from the combo box (see picture below)
Existing table can be edit via icon Table composer  or via double clicking on the header of the table, see picture above
or via double clicking on the header of the table, see picture above
The following values can be presented in numerical output:
|
Value |
Explanation |
|
Nu |
Factored axial normal force |
|
Muy |
Factored bending moment around y axis (with influence of slenderness effect, if is taken into account) |
|
Muz |
Factored bending moment around z axis (with influence of slenderness effect, if is taken into account) |
|
db |
Nominal diameter of longitudinal bar |
|
#bars |
Number of needed bars |
|
As,add |
Theoretical reinforcement area (additional required area which is required to be added to user defined reinforcement to cross-section satisfies) |
|
As,perc |
Percentage of longitudinal reinforcement in whole cross-section |
|
Reinfreq |
Number of required reinforcement bars (required number of bars which is required to be added to user defined reinforcement to cross-section satisfies). For rectengular column: String: nreq(nreq,y /n nreq,z )x db, for example 20(12/12)x0,5 For other column: String: nreqx db, for example 20x0,5 nreq,y – number of bars of required reinforcement in direction y nreq,z – number of bars of required reinforcement in direction z nreq – total number of bars of required reinforcement nreq = nreq,y + nreq,z – 4 |
|
Calc. type |
Column calculation type: Us = uni-axial(sum) (diagram), Um = uni-axial(max) (diagram), B = bi-axial (formula), N/A = Not available, C = Circle column, O = Only corner design |
|
Ratio y/z |
Ratio of reinforcement in y and z direction calculated for designed area |
|
Interaction check |
Result of the interaction formula (Only for biaxial calculation ) |
|
W/E |
Number that refers to the list of typical errors |
|
Φ |
Strength reduction factor |
|
As,req,cor |
Required reinforcement area in corner of rectangular cross-section (it is always reinforcement area of 4 bars) |
|
As,req,ed,y |
Required reinforcement area on edges in y direction (only for rectangular cross-section) |
|
As,req,ed,z |
Required reinforcement area on edges in z direction (only for rectangular cross-section) |
|
As,req,y |
Required reinforcement area in y direction (only for rectangular cross-section) As,req,y = As,req,ed,y +0,5· As,req,cor |
|
As,req,z |
Required reinforcement area in z direction (only for rectangular cross-section) As,req,z = As,req,ed,z +0,5· As,req,cor |
|
As,req |
Required reinforcement area As,req = As,req,y + As,req,z |
|
As,user,cor |
User reinforcement area in corner (only for rectangular cross-section). It is always reinforcement area of 4 bars) |
|
As,user,ed,y |
User reinforcement area on edges in y direction (only for rectangular cross-section) |
|
As,user,ed,z |
User reinforcement area on edges in z direction (only for rectangular cross-section) |
|
As,user,y |
User reinforcement area in y direction (only for rectangular cross-section) As,user,y = As,user,ed,y + 0,5·As,user,cor |
|
As,user,z |
User reinforcement area in z direction (only for rectangular cross-section) As,user,z = As,user,ed,z + 0,5·As,user,cor |
|
As,user |
User reinforcement area As,user = As,user,y + As,user,z |
|
Reinfcor |
Number of reinforcement bars in corner (only for rectangular column). Content: 4 x db(As,user,cor) + 4x db(As,req,cor) for example 4x0,5 (0,79) + 4x0,5 (0,79) |
|
Reinfed,y |
Number of reinforcement bars on edges in direction y (only for rectangular column) String: nuser,ed,y x db(As,user,ed,y)+nreq,ed,y xdb(As,user,ed,y),for example 6x0,5(1,17)+4x0,5 (0,79) nreq,ed,y – number of bars of required reinforcement on edges in direction y nuser,ed,y – number of bars of user reinforcement on edges in direction y |
|
Reinfed,z |
Number of reinforcement bars on edges in direction y (only for rectangular column) String: nuser,ed,z x db(As,user,ed,z)+nreq,ed,z xdb(As,user,ed,z),for example 4x0,5(0,79)+4x0,5 (0,79) nreq,ed,z – number of bars of required reinforcement on edges in direction z nuser,ed,z – number of bars of user reinforcement on edges in direction z |
|
Reinfy |
Number of reinforcement bars in direction y (only for rectangular column) String: nreg,y x db(As,user,y)+nuser,y xdb(As,req,y),for example 8x0,5(1,58)+6x0,5 (1,17) nreq,y – number of bars of required reinforcement on edges in direction y: nreq,y = nreq,ed,y+2 nuser,y – number of bars of user reinforcement on edges in direction y: nuser,y = nuser,ed,y+2 |
|
Reinfz |
Number of reinforcement bars in direction z (only for rectangular column) String: nreg,z x db(As,user,z)+nuser,z xdb(As,req,z),for example 8x0,5(1,58)+6x0,5 (1,17) nreq,z – number of bars of required reinforcement on edges in direction z: nreq,z = nreq,ed,z+2 nuser,z – number of bars of user reinforcement on edges in direction z: nuser,z = nuser,ed,z+2 |
|
Reinftot |
Total number of reinforcement bars String: nreg x db(As,user)+nuser xdb(As,req,),for example 8x0,5(1,58)+6x0,5 (1,17) nreq– number of bars of required reinforcement (for rectangular column nreq = nreq,y + nreq,z ) nuser – number of bars of user reinforcement : (for rectangular column nreq = nreq,y + nreq,z ) |
|
Design Type |
Design calculation type: UI = User input of value Phi, IC = Iterative calculation of value Phi, NC = Non-iterative calculation of value Phi, ND = Not defined |
|
Poy |
Axial resistance for bending moment Mu (Only for biaxial calculation, Bresler reciprocal method ) |
|
Poz |
Axial resistance for bending moment Muz (Only for biaxial calculation, Bresler reciprocal method ) |
|
Po |
Maximum axial resistance without bending moments (Only for biaxial calculation, Bresler reciprocal method ) |
|
Mnoy |
Nominal uniaxial moment resistance about the local y-axis of the member (Only for biaxial calculation, Bresler and PCA load contour method ) |
|
Mnoz |
Nominal uniaxial moment resistance about the local z-axis of the member (Only for biaxial calculation, Bresler and PCA load contour method ) |
|
εst |
Max. tension strain in reinforcement |
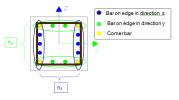
The values in graphical output is always presented around axis of LCS , if the item More comp from combo box Values is not selected. If the item More comp. is selected, then user can select if the values will be presented around local axis (Drawing = 3D) or in one plane (Drawing = Screen)
|
Drawing = 3D |
Drawing = Screen |
|---|---|
8.2.2.2.2 Only corner design
This method is used for design of longitudinal reinforcement:
- For member without concrete member data, if check box Only corner design is ON in Concrete setup (General > Calculation > tab-sheet Columns), see chapter "4.1 Concrete setup for 1D member"
- For member with concrete member data, if check box Only corner design is ON in Concrete member data, see chapter "5.2 Member data 1D (beams, beams as slab, columns)"
Only corner design is special type of calculation, where the reinforcement is designed only in corner of cross-section with internal angle 90deg. It is an iterative calculation, where number of bars is same, but the diameter of bars increases. The way of increasing diameter depends on setting of radio button Design reinforcement by using (biaxial and only corner design) in Concrete setup, item Calculation > Column > Advanced setting, see chapter 4.1.3.1.5.7 Group Design reinforcement using (biaxial and only corner design)
- For real are of reinforcement bars – the diameter of bar increases according to list of basic diameters, which can be different for each code. For ACI code the list of diameter depends on measuring system, see chapter "2 Setting of calculation – units and measuring system" and table below. The initial value of diameter for calculation is loaded from concrete setup ( item Design default > Column, see chapter "4.1 Concrete setup for 1D member"), if concrete member data is not defined or from concrete member data ( see chapter "5.2 Member data 1D (beams, beams as slab, columns)") otherwise. The iteration calculation is finished, when cross-section satisfies for ULS check.
|
Diameter d |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
Imperial [inch] |
0.375 |
0.5 |
0.625 |
0.75 |
0.875 |
1 |
1.128 |
1.27 |
1.41 |
1.693 |
2.257 |
- |
- |
- |
- |
|
Soft metric [inch] |
9.5 |
12.7 |
15.9 |
19.1 |
22.2 |
25.4 |
28.7 |
32.3 |
35.8 |
43 |
57.3 |
- |
- |
- |
- |
|
European [mm] |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
22 |
25 |
26 |
28 |
30 |
32 |
40 |
- For delta area of reinforcement – the diameter of bar is calculated from input value of delta area. The value delta area represents increasing area of one bar of reinforcement in each iteration step. The diameter of bars in each iteration step is calculated according to formula below and it is rounded up to integer number. The initial value of diameter for calculation is calculated according to formula below for first iteration step (i =1). The iteration calculation is finished, when cross-section satisfies for ULS check.

|
where |
|
|
ΔA |
is value of delta area set in concrete setup, see chapter 4.1.3.1.5.7.2 Delta area of reinforcement |
|
i |
is number of iteration step |
In both cases the calculation finishes with error 508 (The number of iteration is exceeded) if designed reinforcement does not satisfy for maximum diameter defined in table above.
The position of corner bars in both cases is calculated from parameters defined in concrete setup (item Design default > Column, see chapter "4.1 Concrete setup for 1D member"), if concrete member data is not defined or from concrete member data (see chapter "4.1 Concrete setup for 1D member") otherwise. The position is not changed during the iteration calculation.
Only the basic concrete section (Cross-section > Concrete) is supported for this calculation. The number of bars (ns) depends on shape of cross-section
|
Section |
Rectangular section |
I section |
T section |
L section with lower flange |
L section with upper flange |
|
ns |
4 |
8 |
6 |
5 |
5 |
|
Shape |
In the table below is designed longitudinal reinforcement to columns with different shape of cross-section loaded by compressive axial force and biaxial bending moment with using method Only corner design (initial value of diameter is 12 mm).
8.2.2.2.3 Uniaxial bending calculation
This method is available only for rectangular cross-section and there is supported two types of Uniaxial bending calculation:
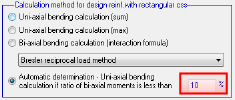
- Uniaxial bending calculation (sum) - this method is used for design of longitudinal reinforcement for member (column) without concrete member data, if Calculation method for design reinf. with rectangular css = Uniaxial bending calculation(sum) in Concrete setup (General > Calculation > column > Advanced), see chapter "4.1 Concrete setup for 1D member" and for member with concrete member data, if Type of calculation = Uniaxial (sum), see chapter "5.2 Member data 1D (beams, beams as slab, columns)" . The longitudinal reinforcement is designed in both direction and resultant area is sum of area from both directions (As = Asy+Asz)
- The area of reinforcement in y axis Asy is calculated for axial force (Pu/φ) and bending moment about y axis (Muy/φ) of LCS of column
- The area of reinforcement in z axis Asz is calculated for axial force (Pu/φ) and bending moment about z axis (Muz/φ) of LCS of column
|
Uniaxial bending moment (sum) |
|||
|
Direction |
y axis |
z axis |
Resultant |
|
Dimensional forces |
Pu/φ, Muy/φ |
Pu/φ, Muyz/φ |
Pu/φ, Muy/φ, Muyz/φ |
|
Arae of reinforcement |
Asy |
Asz |
As = Asy+Asz |
|
Picture |
|
|
|
- Uniaxial bending calculation (max) - this method is used for design of longitudinal reinforcement is used for member (column) without concrete member data, if Calculation method for design reinf. with rectangular css = Uniaxial bending calculation(max) in Concrete setup (General > Calculation > column > Advanced), see chapter "4.1 Concrete setup for 1D member" and for member with concrete member data, if Type of calculation = Uniaxial (max) ,see chapter "5.2 Member data 1D (beams, beams as slab, columns)". The longitudinal reinforcement is designed only for axial load (Pu/φ) and one bending moment (maximum of bending moment about y axis (Muy/φ) and z axis (Muz/φ) of LCS)
|
Uniaxial bending moment (max) |
||
|
Condition |
Muy ≥ Muz |
Muy < Muz |
|
Dimensional forces |
Pu, Muy |
Pu, Muz |
|
Area of reinforcement |
As = Asy |
As = Asz |
|
Picture |
|
|
Uniaxial calculation is taken into account if check box Only corner design in concrete setup or in concrete member data is OFF
The procedure of design of longitudinal reinforcement is based on the calculation of equilibrium between internal forces and external load. The following preconditions are used
- Plane section remains plane after loading (deformation) too
- Tensile strength of concrete is not taken into account (cracked section)
- ideal bond between concrete and reinforcement is taken into account, it means change strain of reinforcement εs and concrete fibber εc in the same position is the same
Parabola-rectangle strain-stress diagram for concrete is used
Bilinear strain-stress diagram with or without inclined top branch can be used
The reinforcement is always symmetrical above y(z) axis of local coordinate system of the column.
In the table below are compared results of design reinforcement with using Uniaxial bending calculation (sum) and Uniaxial bending calculation (max) for column with different values of bending moments Muy and Muz.
|
Uniaxial (sum) |
|
|
Uniaxial (max) |
8.2.2.2.4 Biaxial bending calculation for rectangular column
This method is available only for rectangular cross-section and is used for member (column) without concrete member data, if Calculation method for design reinf. with rectangular css = Biaxial bending calculation(interaction formula) in Concrete setup (General > Calculation > column > Advanced), see chapter "4.1 Concrete setup for 1D member" and for member with concrete member data, if Type of calculation = biaxial , see chapter "5.2 Member data 1D (beams, beams as slab, columns)".
Biaxial calculation is taken into account if check box Only corner design in concrete setup or in concrete member data is OFF
It is an iterative calculation, where number of bars is changed. The way of increasing number of bars of reinforcement in direction of y and z axis of LCS in each step depends on ratio of reinforcement in y and z direction of LCS of the column (see chapter 4.1.3.1.5.9 Group Ratio y/z or "5.2 Member data 1D (beams, beams as slab, columns)") and on results of interaction formula. At first initial check of interaction formula for minimum number of bars is checked, it mean one bar in each corner of rectangular column. If interaction formula satisfies, the calculation is finisher. Otherwise iterative calculation according to scheme below is used.
|
where |
|
|
nin |
The initial number of bars in one edge of rectangular cross-section. Default value is 32 |
|
ny(z) |
number of bars at one edge of rectangular cross-section in y or z direction of LCS of the compression member |
|
ratio_y/z |
Ratio of reinforcement in y and z direction of LCS of compression member for biaxial calculation. Three type of method for calculation of this ratio are supported and this method and value can be set:
|
The number of bars in direction of z and y axis of LCS of compression member does not depend on value ratio_y/z (the scheme above is not used), if check box Optimize the number of bars in c-s for biaxial calculation (Concrete setup > General > Calculation, see chapter "4.1 Concrete setup for 1D member" ) is ON. In this case program checked all possible arrangements of bars of reinforcement in z and y directions and select this one, which result of interaction formula is the nearest to one
If it is not possible to input designed number of bars too cross-section (problem with minimum bars distance) during to iterative calculation, the program finishes with warning 115 (Maximum number of bars was placed into cross-section and the design basic condition is not fullfiled)
The area of one reinforcement bar used in biaxial calculation depends on setting of radio button Design reinforcement by using (biaxial and only corner design) in Concrete setup, item Calculation > Column > Advanced setting, 4.1.3.1.5.7 Group Design reinforcement using (biaxial and only corner design)
- For real area of reinforcement bars – diameter of bar for calculation area of one reinforcement bar is loaded from concrete setup (item Design default > Column, see chapter "4.1 Concrete setup for 1D member"), if concrete member data is not defined or from concrete member data (see chapter "5.2 Member data 1D (beams, beams as slab, columns)") otherwise.
- For delta area of reinforcement – the area of one bar is loaded from concrete setup (Concrete setup > General > Calculation > Advanced setting > delta area of reinforcement), see chapter 4.1.3.1.5.7.2 Delta area of reinforcement
In both cases the number of bars from designed area of reinforcement area calculated from the diameter defined in concrete setup, if member data is not defined on the member or from diameter defined in concrete member data, if member data is defined.
Three type methods (interaction formula) can be used for biaxial calculation of rectangular cross-section. This type of method can be set
- For member without concrete member data in concrete setup via group Calculation method for design reinf. with rectangular css (Concrete setup > General > Calculation > Advanced setting), see chapter "4.1 Concrete setup for 1D member"
- For member with concrete member data in concrete member data via combo box Method of calculation, "5.2 Member data 1D (beams, beams as slab, columns)"
|
Method |
Interaction formula |
|---|---|
|
Bressler reciprocal load method |
|
|
Bressler load contour method |
|
|
PCA load contour method |
|
|
where |
|
|
Pu/φ |
factored axial force |
|
Poy |
Maximum uniaxial resistance of the column with a moment of Muy/φ, it means axial resistance for bending moment Muy/φ .It is intersection of Pn-Mn diagram and vertical line ( parallel with axis P) across the point with coordinate [Pu/φ, Muy/φ,0] |
|
Poz |
Maximum uniaxial resistance of the column with a moment of Muz/φ, it means axial resistance for bending moment Muz/φ. It is intersection of Pn-Mn diagram and vertical line ( parallel with axis P) across the point with coordinate [Pu/φ,0, Muz/φ] |
|
Po |
Is maximum axial resistance without bending moments. It is intersection of interaction diagram and vertical line ( parallel with axis P) across the point with coordinate [Pu/φ,0, 0] |
|
Muy(z)/ φ |
Factored (magnified) moment at section about the y (z) axis of LCS of the member |
|
f |
Strength reduction factor calculated by iterative calculation, loaded from concrete setup or from concrete member data, see chapter "4.1 Concrete setup for 1D member" |
|
Mnoy(z) |
nominal uniaxial moment resistance about the y (z) axis of LCS of the member |
|
α |
Exponent of interaction formula, which can be set in concrete setup, 4.1.3.1.5.8.1 Alpha |
|
b |
Exponent of interaction formula, which can be set in concrete setup, 4.1.3.1.5.8.2 Beta |
In the table below are compared results of design reinforcement with using Biaxial bending calculation (interaction diagram) for column with rectangular cross-section and for different methods.
|
Input data |
b =12 inch; h=20inch;c=1.5 inch; Pu=197,4 kip; Muy =129,8kipft; Muz =76kipft 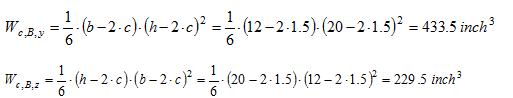
σy =Muy/Wc,B,y =129.8/433.5 =0.00358 ksi ; σz =Muz/Wc,B,z =76/229.5 =0,003974 ksi Ratio y/z = |
|
Result |
|
|
Bressler reciprocal load method |
Initial check with minimum number of bars satisfies, iterative calculation is not necessary
|
|
Bressler load contour method α = 1.5 |
Initial check with minimum number of bars does not satisfy, iterative calculation is necessary |
|
PCA load contour methodβ = 0.65 |
Initial check with minimum number of bars does not satisfy, iterative calculation is necessary |
Design of reinforcement for circular column
This method is used for column with circular cross-section and for this cross-section is always used the following interaction formula
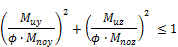
|
where |
|
|
Muy(z)/ φ |
Factored (magnified) moment at section about the y (z) axis of LCS of the member |
|
f |
Strength reduction factor calculated by iterative calculation, loaded from concrete setup or from concrete member data, see chapter "4.1 Concrete setup for 1D member" |
|
Mnoy(z) |
nominal uniaxial moment strength about the y (z) axis of LCS of the member |
It is an iterative calculation, where number of bars is changed. The way of increasing number of bars in each steps depends on result of interaction formula, see scheme below
In the table below is presented iterative calculation and result of design reinforcement for column with circular cross-section.
|
Result |
|
|
Iterative calculation |
8.2.2.2.6 Automatic calculation
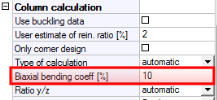
This automatic determination of method for design reinforcement is supported only for rectangular column and it is used
- for member without concrete member data, if Calculation method for design reinf. with rectangular css = Automatic determination in Concrete setup (General > Calculation > column > Advanced), see chapter "4.1 Concrete setup for 1D member"
- for member with concrete member data, if Type of calculation = automatic, see chapter "5.2 Member data 1D (beams, beams as slab, columns)"
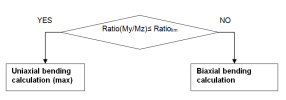
Type of method, which will be used for design reinforcement, if Calculation Method =Automatic determination is selected, depends on ratio bending moments.
Ratio(My/Mz) = 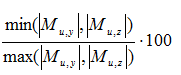
|
where |
|
|
Muy(z)/ φ |
Factored (magnified) moment at section about the y (z) axis of LCS of the member |
|
Ratiolim |
Limit value of ratio biaxial bending moment, which can be set
|
|
Member without concrete member data |
Member with concrete member data |
There is comparison of results for automatic determination of calculation moment for column with different value of bending moment column with the same load, but with different size of diameter of longitudinal reinforcemen.
If bending moments in both direction are zero, then reinforcement is designed only for normal force and calculation type =N/A
8.2.2.2.7 Detailing provisions
The following detailing provisions are checked for longitudinal reinforcement
Minimum percentage of reinforcement
Maximum percentage of reinforcement
Minimum clear bars spacing
Minimum number of bars
8.2.2.2.7.1 Min. reinf. percentage
This detailing provisions is taken into account for design of reinforcement, if check box Min. reinf. percentage is ON (Concrete setup > Detailing provisions > Columns ), see chapter 4.1.5.2.1.1 Min. reinf. percentage. If this check box is ON and area of longitudinal reinforcement is lesser than minimum area of reinforcement.
As = As,min = x·Ag /100
then design of longitudinal reinforcement finishes with error 2 (The main reinforcement area was designed according to min. Required reinforcement percentage)
|
where |
|
|
Ag |
gross area of concrete section |
|
x |
Value of minimum percentage loaded from edit box |
The minimum diameter of longitudinal reinforcement for Corner design only which can be used in calculation, if this detailing provisions ON, is calculated according to formula:
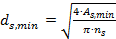
|
where |
|
|
ns |
number of bars depending on shape of cross-section, see chapter Only corner design |
The recalculation minimum area of reinforcement to direction y (area Asy) and z (area Asz) of LCS of rectangular compression member depends on type of calculation and values of bending moments
|
Type of calculation |
Bending moments |
Asy | Asz | |
|---|---|---|---|---|
|
Uni-axial calculation |
Muy =0 |
Muz =0 |
0,5·As,min |
0,5·As,min |
|
Muy ≠ 0 |
Muz =0 |
As,min |
0 |
|
|
Muy = 0 |
Muz ≠0 |
0 |
As,min |
|
|
Muy ≠0 |
Muz ≠0 |
0,5·As,min |
0,5·As,min |
|
|
Bi-axial calculation |
- |
- |
0,5·As,min |
0,5·As,min |
Percentage of reinforcement can be presented graphically and numerically, if in service Design As value Reinforcement ratio is selected
There is presented minimum area of reinforcement for different shape of cross-section and automatic determination of method for rectangular column.
8.2.2.2.7.2 Max. reinf. percentage
This detailing provision is taken into account for design of reinforcement, if check box Max. reinf. percentage is ON (Concrete setup > Detailing provisions > Columns), see chapter 4.1.5.2.1.2 Max. reinf. percentage. If this check box is ON and area of longitudinal reinforcement is greater than maximum area (As > As,max = x·Ag /100). Then design of longitudinal reinforcement finishes with warning 502 (The percentage of designed reinforcement is higher than the maximum percentage))
|
where |
|
|
Ag |
gross area of concrete section |
|
x |
Value of maximum percentage loaded from edit box |
8.2.2.2.7.3 Mini clear bars spacing
This detailing provisions is taken into account for design of reinforcement, if one from two check boxes Min.clear bars spacing is ON (Concrete setup > Detailing provisions > Columns ), see chapter 4.1.5.2.1.3 Min. clear bars spacing or 4.1.5.2.1.4 Min. clear bars spacing .
|
Setting of calculation |
Minimum clear bars spacing |
|
|
|
|
|
|
|
|
|
where |
|
|
db |
diameter of longitudinal reinforcement loaded
|
|
x,y |
Values of minimum clear distance loaded form edit boxes, see chapter 4.1.5.2.1.3 Min. clear bars spacing or 4.1.5.2.1.4 Min. clear bars spacing
|
If one from check boxes for check minimum clear bars spacing is ON and the clear bars spacing between bars is lesser than minimum, program finishes with the following warning:
|
Warning |
Description |
Cause |
|---|---|---|
|
134 |
Tha bar distance for the Y-direction is too small |
The minimum spacing of bars in direction of y-axis of LCS of the member for rectangular cross-section does not satisfy |
|
136 |
Tha bar distance for the Z-direction is too small |
The minimum spacing of bars in direction of z-axis of LCS of the member for rectangular cross-section does not satisfy |
|
138 |
The bars distance is too small |
The minimum spacing of bars in circular cross-section is does not satisfy |
Minimal clear distance between bars is set as
The minimum spacing of bars is not checked for Only corner design
If for biaxial calculation , it is not possible to input designed number of bars too cross-section (problem with minimum bars distance) during to iterative calculation, the program finishes with warning 115 (Maximum number of bars was placed into cross-section and the design basic condition is not fullfiled)
8.2.2.2.7.4 Max. bars spacing
This detailing provisions is taken into account for design of reinforcement, if check box Max.bars spacing is ON (Concrete setup > Detailing provisions > Columns ), see chapter 4.1.5.2.1.5 Max. bars spacing . If this check box is ON, then centre-centre spacing between bars is checked. This is code independently check. If this centre-centre spacing of bars is bigger than maximum spacing then design of longitudinal reinforcement finishes with the following warnings
|
Warning |
Description |
Cause |
|---|---|---|
|
133 |
Tha bar distance for the Y-direction is too big |
The centre-centre maximum spacing of bars in direction of y-axis of LCS of the member for rectangular cross-section does not satisfy |
|
135 |
Tha bar distance for the Z-direction is too big |
The centre-centre maximum spacing of bars in direction of z-axis of LCS of the member for rectangular cross-section does not satisfy |
|
137 |
The bars distance is big |
The centre-centre maximum spacing of bars in circular cross-section does not satisfy |
The maximum spacing of bars is not checked for Only corner design
8.2.2.2.7.5 Minimum number of bars
This detailing provisions is taken into account for design of reinforcement, if check box Min.number of bars is ON (Concrete setup > Detailing provisions > Columns), see chapter 4.1.5.2.1.6 Min. number of bars . If this check box is ON, then in design of reinforcement minimum number of bars set in concrete setup is used for design of reinforcement, though number of bars of statically required reinforcement is lesser. For rectangular column minimum numbers of bars is always 4, independently on value defined in the concrete setup. This check is used for circular column.
8.2.2.3 Shear reinforcement
Transverse (shear) reinforcement is designed as ties and vertical spacing of ties is designed according to detailing provisions. The same shape of cross-section are supported for shear reinforcement as for longitudinal reinforcement
- Rectangular cross-section
- Circular cross-section
- T-shape, L-shape and I shape of cross-section, if Only corner design of longitudinal reinforcement is used, see chapter Only corner design
The results of shear reinforcement is presented in numerical and graphical output and detailed results for each section can be presented via action button Single check
The numerical output is available after clicking on action button Preview. The numerical output of shear reinforcement is presented, if values Ass is selected
8.2.2.3.1 Design of shear reinforcement
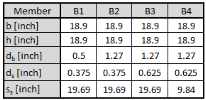
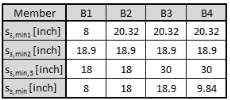
The vertical spacing of ties depends on:
- maximum spacing, which is in concrete setup (Detailing provisions > Columns > Transverse reinforcement) via three values. These values are not taken into account , if check boxes for these values below are OFF.
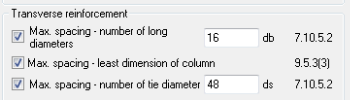
- max.spacing – number of long diameter (ss,min,1 = x·db ), see chapter 4.1.5.2.2.1 Max.spacing – number of long diameter
- max.spacing – least dimension of column (ss,min,2 = min (b;h)), see chapter 4.1.5.2.2.2 Max.spacing – least dimension of column
- max. spacing - number of tie diameter (ss,min,3 = x·ds), see chapter 4.1.5.2.2.3 Max.spacing – number of tie diameter
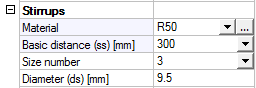
- basic distance (ss) defined in concrete member data, see chapter "5.2 Member data 1D (beams, beams as slab, columns)" . This basic distance is not taken into account, if zero value is set.
|
Maximum spacing defined in Concrete setup |
Basic distance in concrete data |
The final vertical spacing of ties are calculated according to formula:
| ss,min = min | ss,min,1 = x·db if check box is ON |
| ss,min,2 = min (b;h) if check box is ON | |
| ss,min,3 = x·ds if check box is ON | |
| ss if ss≠ 0 |
The area of shear reinforcement per meter is calculated according to formula
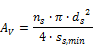
|
where |
|
|
db |
diameter of longitudinal reinforcement loaded
|
|
ds |
diameter of shear reinforcement (tie diameter)
|
|
b,h |
The dimensions of cross-section of compression member in direction of y(z) axis of LCS. For different shape of cross-section as than rectangular shape, the dimensions of circumscribed rectangular is taken into account |
|
x |
values of maximum spacing loaded from edit box |
|
ns |
Number of cuts of ties, which can be calculated :
|
|
bcen |
width of cross-section in centroid of concrete cross-section |
|
hcen |
height of cross-section in centroid of concrete cross-section |
|
c |
The nominal value of concrete cover, value presented in property Concrete cover |
|
st,max |
the maximum transverse spacing of the legs, the value is defined in concrete setup (Concrete setup > Detailing provisions >Columns >Transverse reinforcement), see chapter 4.1.5.2.2.5 Max transverse spacing of the legs |
The diameter of longitudinal reinforcement for calculation of vertical spacing of shear reinforcement is always loaded from concrete setup or concrete member data, though diameter of this longitudinal reinforcement is increased during Only corner design
In the table below is presented results of calculation vertical spacing of ties for compression member with different input data
|
Input data and manually calculation |
|
|
Results in SEN |
8.2.2.3.2 Detailing provisions
Shear reinforcement is designed according to detailing provisions – maximum vertical spacing. Except the program is able to check minimum value of diameter of shear reinforcement.
8.2.2.3.2.1 Check diameter of shear reinforcement
This detailing provisions is taken into account for design of shear reinforcement, if check box Check diameter is ON (Concrete setup > Detailing provisions > Columns), see chapter 4.1.5.2.2.4 Check diameter. If this check box is ON, then minimum diameter of shear reinforcement (ties) according to clause 7.10.5.1 in ACI 318-05 is checked during design of shear reinforcement. Minimum diameter of shear reinforcement depends on diameter of longitudinal reinforcement, which enclosed, see table below
|
Unit format |
Diameter of longitudinal reinforcement |
Minimum shear diameter |
|
US |
|
|
|
|
|
|
|
Metric |
|
|
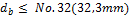
|
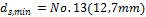
|
|
where |
|
|
db |
diameter of longitudinal reinforcement loaded
|
The diameter of longitudinal reinforcement for calculation of vertical spacing of shear reinforcement is always loaded from concrete setup or concrete member data, though diameter of this longitudinal reinforcement is increased during Only corner design
If diameter of shear reinforcement is lesser than minimum shear diameter, then design of shear reinforcement with warning 163 (The profile diameter of shear reinforcement is lesser than permitted). In this case, value shear reinforcement has to be increased in :
- concrete setup (Design default > Column >Stirrup), if member data is not defined on the member or
- concrete member data (Design > Stirrups >Diameter) , if concrete member data is defined on the member

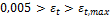
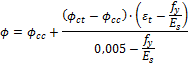
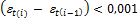 (value from concrete setup
(value from concrete setup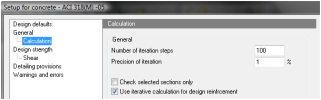
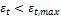




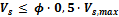
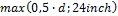
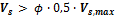

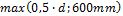
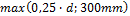
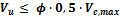
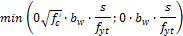
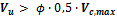
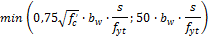
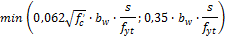


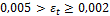
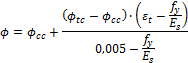
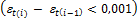 or number of iteration setup is exceeded
or number of iteration setup is exceeded