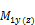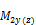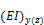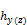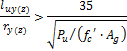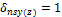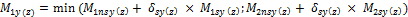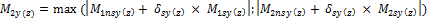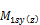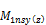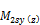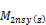7.2 Internal forces for 1D members (beam, beam as slab, column)
There is different evaluation according to type of member (beam, beam as slab, column). Each type of member has special settings which can affect the internal forces used for design of reinforcement.
7.2.1 Beams and beam as slab
Recalculated internal forces are dependent on
strength reduction factor for bending (see chapter "8.2 Design of reinforcement for 1D members (beams, beams as slab, columns)" for more information about used method and this factor) and for shear which is usually 0,75
capping of moment and shear forces (dependent on settings used in concrete setup or concrete member data
7.2.1.1 Strength reduction factors and internal forces
There are used two types of internal forces during design of reinforcement
Factored internal forces (Xu) – internal forces from statical analysis
Nominal internal forces (Xn) – internal forces with respect of strength reduction factor
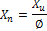
Generally it is required to use strength reduction factor on side of the material strength, but we don’t know phi factor before design starts (see different method in chapter "8.2 Design of reinforcement for 1D members (beams, beams as slab, columns)"). That’s why the strength reduction factor is used on side of increasing of the load instead of the decreasing of the strength.
There are used different strength reduction factors for bending and for shear. The default limits are set in Concrete setup>Design strength (see chapter "4 Global setting ").
7.2.1.1.1 Bending, tension, compression
Strength reduction factor for bending is used according to used method described in chapter "8.2 Design of reinforcement for 1D members (beams, beams as slab, columns)". There are two limits for:
Tensioned controlled section 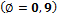 - in case when strain of reinforcement is higher than 0,005
- in case when strain of reinforcement is higher than 0,005
Compression controlled section 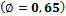 - in case when strain of reinforcement is lower than 0,002
- in case when strain of reinforcement is lower than 0,002
Transition zone – special zone where linear interpolation according to calculated strain in reinforcement between tension controlled section and compression controlled section is applied
7.2.1.1.2 Shear
Strength reduction factor used for shear is fixed and it is equal to 0,75 all the time.
7.2.1.2 Capping above support
The capping above the support is another effect which influences the values of internal forces used for design of reinforcement. There are two types of capping – moment and shear capping.
7.2.1.2.1 Moment capping
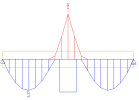
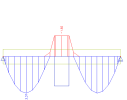
Moment capping reduces the peaks of the bending moment above the supports. The reducing depends on width of the supports where reducing is applied on. Width of the support is taken into account dependent on existence of Concrete member data.
|
CMD |
Support width |
|
NO
|
|
|
YES
|
The comparison of the bending moments with and without capping for standard support and for column support is done in the following table.
|
Moment capping |
NO |
YES |
|---|---|---|
|
Standard support |
||
|
Column support |
7.2.1.2.2 Shear force capping
Shear capping is another possibility of capping used for the shear force. There are two types of calculation of reduced shear force depending on settings in Concrete setup.
A) At the face (support/column) - shear force above the support is the same as shear force in the face of the support/column
B) At the effective depth from the face (support/column) – shear force is calculated at distance d (effective depth of cross-section) from the face of support/column
|
Type of shear capping |
Evaluation of shear force |
|---|---|
|
Without capping |
|
|
At the face |
|
|
At the effective depth |
7.2.2 Column
Recalculation bending moment for column can be impacted only by slenderness effect (magnified moments). Magnified moments are calculated only in case that
- slenderness ratio is bigger than lower limit of slenderness ratio and
- slenderness ratio is lesser than upper limit of slenderness and
- check box Use buckling data is ON in Concrete setup (see chapter "4.1 Concrete setup for 1D member") or in concrete member data (if it is defined on the member), see chapter "5.2 Member data 1D (beams, beams as slab, columns)"
Calculation of these magnified moments depends on it, if the member is sway or not. The following formulas are used for calculation:
|
Type of member |
Clause in ACI 318-05 |
Equation |
|---|---|---|
|
Non-sway |
10.12.3 |
Muy(z),rec = max (δnsy(z)⋅ Muy(z); Mminy(z)) |
|
Sway |
10.13.3 |
Muy(z),rec = max (δnsy(z)⋅ Mnsy(z) + δsy(z)⋅ Msy(z); Mminy(z)) |
|
where |
|
|
δnsy(z) |
moment magnification factor about y(z) axis of LCS for member braced against sidesway (non-sway member), to reflect effects of member curvature between ends of compression member, "7.2 Internal forces for 1D members (beam, beam as slab, column)" and "7.2 Internal forces for 1D members (beam, beam as slab, column)" |
|
Muy(z) |
factored moment about y (z) axis of LCS of compression member. It can be calculated according to equation: Muy(z) = Mnsy(z) + Msy(z) |
|
Mminy(z) |
Minimum value of magnified moment about y (z) axis of LCS of compression member, see charter "7.2 Internal forces for 1D members (beam, beam as slab, column)" |
|
Mnsy(z) |
factored moment about y (z) axis of LCS of compression member due to loads that cause no appreciable sidesway |
|
δsy(z) |
moment magnification factor factor about y(z) axis of LCS for member not braced against sidesway (sway member), to reflect lateral drift resulting from lateral and gravity loads, "7.2 Internal forces for 1D members (beam, beam as slab, column)" |
|
Msy(z) |
factored moment about y (z) axis of LCS of compression member due to loads causing appreciable sway |
If the member will be sway or non-sway can be set in dialog Buckling and relative lengths > Buckling data or in dialog Buckling coefficients (member buckling data is defined, user input is selected and kyy(zz) = Code dependent ) via property Swaz zz or Sway zz
The loads cause appreciable sway (load caused factored moment Msy(z)), if the load belong to load case, for which check box Loads cause appreciable sideway is ON in dialog for definition of load cases, see picture below
7.2.2.1 Magnified moments for non sway member
The calculation of magnified moments for non-sway member is calculated according to formula
Muy(z),rec = max (δnsy(z)⋅ Muy(z); Mminy(z)) = max (δnsy(z)⋅( Mnsy(z) + Msy(z)); Mminy(z))
It follows, that magnified moments depends on:
- moment magnification factor for member braced against sidesway (non-sway member), value δnsy(z)
- total value of factored bending moment (sum of factored moment due to loads that cause no appreciable sidesway and factored moment due to loads that cause appreciable sidesway) at calculated section of the column
- minimum value of magnified moments (value Mminy(z) )
7.2.2.1.1 Moment magnification factor for member braced against sidesway
This value is calculated according to equation 10-9 in ACI 318-05
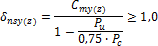
|
where |
|
|
|
factor relating actual moment diagram to an equivalent uniform moment diagram calculated according to clause 10.12.3.1 in ACI 318-05
|
|
|
smaller value of factored end moment on a compression member about y(z) axis of LCS of compression member. The value is positive if member is bent in single curvature, and negative if bent in double curvature |
|
|
larger factored end moment on compression member about y(z) axis of LCS of compression member .The value is usually positive, but the value is negative only in case that both end moments are negative too |
|
Mmax,y(z) |
the maximum value of factored bending moment at whole length of the column |
|
Pu |
factored axial force |
|
Pc |
Critical buckling load calculated according to equation 10-10 in ACI 318-05
|
|
|
stiffness for calculation the critical column load, see chapter 4.1.4.2 Equation for calculation EI for calculation Pc |
|
luy(z) |
System length (unsupported length) of member about y(z) axis of LCS, see chapter 6 Calculation of slenderness |
|
ky(z) |
Effective length factor about y(z) axis of LCS of compression member, see chapter 6 Calculation of slenderness |
If the value 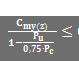 the calculation of magnified moment finishes with error 918 (The compression member is instable, because Pu ≥ 0,75Pc)
the calculation of magnified moment finishes with error 918 (The compression member is instable, because Pu ≥ 0,75Pc)
7.2.2.1.2 Minimum value of magnified moment
This value is calculated according to equation 10-14 in ACI 318-05
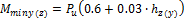
|
where |
|
|
Pu |
factored axial force |
|
|
The dimension of cross-section of compression member in direction of z(y) axis of LCS. For different shape of cross-section as than rectangular shape, the dimensions of circumscribed rectangular is taken into account |
7.2.2.2 Magnified moments for sway member
The calculation of magnified moments for sway member is calculated according to formula
Muy(z),rec = max (δnsy(z)⋅Mnsy(z) + δsy(z)⋅ Msy(z); Mminy(z))
It follows, that magnified moments depends on:
- moment magnification factor for member braced against sidesway (non-sway member), value δnsy(z)
- moment magnification factor for member not braced against sidesway (sway member), value δsy(z)
- factored moment due to loads that cause no appreciable sidesway at calculated section, value Mnsy(z)
- factored moment due to loads causing appreciable sway, see chapter value Msy(z)
- minimum value of magnified moments (value Mminy(z) )
The loads cause appreciable sway (load caused factored moment Msy(z)), if the load belong to load case, for which check box Loads cause appreciable sideway is ON in dialog for definition of load cases, see picture below
7.2.2.2.1 Moment magnification factor for member braced against sidesway
This value is calculated according to clause 10.13.5 in ACI 318-05 and calculation of this factor depends on condition below
|
Condition |
Moment magnification factor |
|---|---|
|
|
|
|
|
|
If the value  the calculation of magnified moment finishes with error 918 (The compression member is instable, because Pu ≥ 0,75Pc)
the calculation of magnified moment finishes with error 918 (The compression member is instable, because Pu ≥ 0,75Pc)
|
where |
|
|
|
factor relating actual moment diagram to an equivalent uniform moment diagram calculated according to clause 10.12.3.1 in ACI 318-05
|
|
|
smaller value of factored end moment on a compression member about y(z) axis of LCS of compression member. The value is positive if member is bent in single curvature, and negative if bent in double curvature
|
|
|
larger factored end moment on compression member about y(z) axis of LCS of compression member. If Else
|
|
Mmax,y(z) |
the maximum value of factored bending moment at whole length of the column |
|
|
factored end moment (at head of compression member) about y (z) axis of LCS of compression member due to loads causing appreciable sway |
|
|
factored end moment (at head of compression member) about y (z) axis of LCS of compression member due to loads that cause no appreciable sidesway |
|
|
factored end moment (at foot of compression member) about y (z) axis of LCS of compression member due to loads causing appreciable sway |
|
|
factored end moment (at foot of compression member) about y (z) axis of LCS of compression member due to loads that cause no appreciable sidesway |
|
δsy(z) |
moment magnification factor about y(z) axis of LCS for member not braced against sidesway (sway member), to reflect lateral drift resulting from lateral and gravity loads, "7.2 Internal forces for 1D members (beam, beam as slab, column)" |
|
Pu |
factored axial force |
|
Pc |
Critical buckling load calculated according to equation 10-10 in ACI 318-05
|
|
|
stiffness for calculation the critical column load, see chapter 4.1.4.2 Equation for calculation EI for calculation Pc |
|
luy(z) |
System length (unsupported length) of member about y(z) axis of LCS, see chapter 6 Calculation of slenderness |
|
ky(z) |
Effective length factor about y(z) axis of LCS of compression member, see chapter 6 Calculation of slenderness |
|
ry(z) |
radius of gyration of cross section about y(z) axis of LCS of compression member, |
|
fc’ |
specified compressive strength of concrete |
|
Ag |
gross area of concrete section |
7.2.2.2.2 Moment magnification factor for member not braced against sidesway
This value is calculated according to equation 10-18 in ACI 318-05, but there is made some simplification of the calculation, where this value is calculated only for individual compression member. It follows:
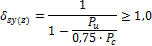
If the value δsy(z) ≥ 2.5 and bending moment due to loads causing appreciable sway is non-zero (Msy(z)≠0), the compression member is instable (clause 10.13.6c in ACI 318-05) and the calculation finishes with error 917 (The compression member is instable, because delta_s ≥ 2.5)
In the formula above is expression ∑Pu (the summation for all the factored vertical loads in a story) substituted by value Pu (factored force at individual compression member ) and expression ∑Pc (the summation critical buckling load for all sway resisting columns in a story) is substituted by value Pc (critical buckling of individual compression member)
7.2.2.2.3 Minimum value of magnified moment
This value is calculated the same as for non-sway member, see chapter "7.2 Internal forces for 1D members (beam, beam as slab, column)"


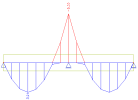
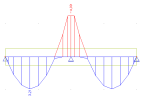

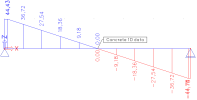
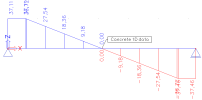
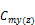
 if Mmax,y(z) ≤ M2y(z) (without transverse load)
if Mmax,y(z) ≤ M2y(z) (without transverse load)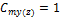 if Mmax,y(z) > M2y(z) (with transverse load)
if Mmax,y(z) > M2y(z) (with transverse load)