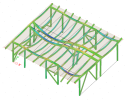
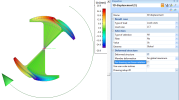
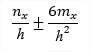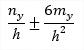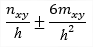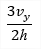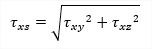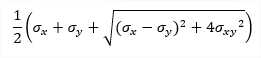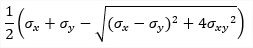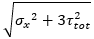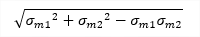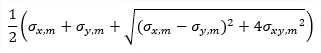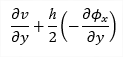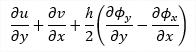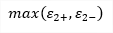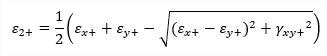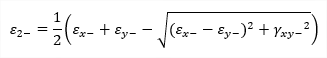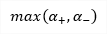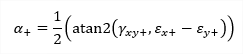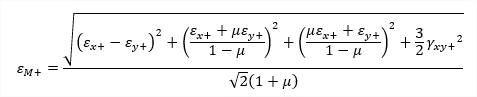3D stress / strain

The 3D stress command serves for displaying stress and strain on selected 1D and 2D members. (not only results from linear and nonlinear analysis, but also stress and strain of modal and stability eigenmodes)

Usage

Calculate a FEM analysis of the model
Go to Tree > Results > 3D stress
Set properties of the command to specify mainly:
- selection of 1D and 2D members where the results are evaluated
- load type from which the results are derived
- specific result value from the available list to be visualized
Click on [Refresh] action button to display the results

Note: To get general overview about how to work with Result service and its commands, see Results/Basics.

Properties

Category	Property	Description / Notes
Selections	Type of selection All / Current / Advanced / Named Selection / Design Group	Specifies on what members the results are displayed See "Type of selection"
	Filter No / Cross-section / Material / WildCard / Layer / Thickness / Type of beam	Specifies the filter of members on what the results are displayed See "Filter"
	Location In nodes no avg. / In nodes avg. on macro	Defines location in finite element mesh of calculated 2D values .
	Trajectories On/Off	Available only for Principal magnitudes / Membrane magnitudes (2D) Displaying results of stresses by trajectories in direction of stress
	Type variables Basic magnitudes / Principal magnitudes / Membrane magnitudes (2D) / Basic total strain (2D) / Principal total strain (2D) / Basic plastic strain (2D) / Principal plastic strain (2D)
	Value	See table Values below.
	System LCS mesh element / Global	Defines in which coordinate system the results are displayed.
	Extreme 1D Fiber / Section / Cross-section / Design group / Member / Global	Defines for which extreme on 1D member the results are displayed.
	Extreme 2D Mesh / Surface / Member / Global	Defines for which extreme on 2D member the results are displayed.
Result case	Type of load Load case / Combinations / Classes / Nonlinear Combinations/ Stability Combinations / Mass combinations	Defines for what load the results are displayed. See"Result case"
Result case	Envelope (for 2D drawing) Minimum / Maximum / Absolute extreme
Calculate results on ...	1D members On / Off	It is possible to switch ON/OFF drawing of results on 1D members or faces of 2D members. positive faceis the face which is on +z local coordinate of the 2D member negative face is on -z local coordinate of the 2D member
	2D positive face On / Off
	2D negative face On / Off
Deformed structure	Deformed structure On / Off	The result values can be displayed also on deformed surface of the structure The deformed surface is displayed for the combination from selected result case which provides the extreme value of selected magnitude. In case the result type contains envelope combination (different combinations can give extreme values for each member of the structure) it is possible to select between "Member deformation for global / local maximum". Note: Member deformation for global maximum means that the deformation of surfaces is calculated just for one exact combination which gives global extreme of selected magnitude. Member deformation for member maximum means that the extreme combination is evaluated for each member separately. In this case the deformed surface can be displayed for different combinations per each member and there can be discontinuities in deformed surface.
Deformed structure	For drawing use linear rotation On / Off	Enables to switch between small displacement assumption based linear translations (which provides result consistent with used assumption) and circular translations (which keeps the original shape of cross section). Linear translation ON / OFF
Drawing Setup 2D		"Drawing setup 2D"
Errors, warnings and notes settings		"Errors, warnings and notes settings"

Values

The following categories of stresses and strains can be displayed:

Note: As default, the stresses and strains refer to the local axes of the individual finite (mesh) elements. The local axes can be displayed by selecting the corresponding option in the View parameters settings.

Basic magnitudes

The basic stresses are default magnitudes referring to the local axes of the selected coordination system.

Value	Description	Notes
σ_x(1D/2D)	stress in direction of local axis x	It is calculated on assumption of linear distribution of the strain within the section. In the first step the plane of deformation is calculated using iterative algorithm () so strain in all fibres is known. In the next step adequate stresses are assigned using stress-strain curve. Remember that linear calculation uses linear approximation (E modulus) of stress-strain curve.
σ_y(2D)	stress in direction of local axis y
t_xy(2D)	shear stress
t_xz(2D)	shear stress perpendicular to the plane
t_yz(2D)	shear stress perpendicular to the plane
t_xy/t_xs(1D)	shear stresses in local coordinates (thick walled cross sections) or total shear flow (thin walled cross sections)	They are calculated from the shear force and torsional moment using unit distribution of shear stresses. Those unit distributions of shear stresses are also available in the cross section editing dialogue. The t_xs magnitude represents the total shear flow which is in the thin-walled cross section. Distribution of this shear flow from horizontal a vertical unit shear forces can be checked in the cross section manager. The shear stresses are evaluated differently for thick-walled and thin-walled cross section. For thick-walled (solid) sections the real t_xyor t_xzare calculated and displayed. For thin-walled sections the final shear flow from unit forces in Y or Z directions are evaluated and displayed as total shear flow: See also chapters in manual related to calculation of sectional characteristics.
t_xz/t_xs(1D)
t_tor/t_xs(1D)

Principal magnitudes

The principal stresses represent the extreme values of the internal forces derived from the basic ones by transformation into the directions of principal axes:

Value	Description	Notes
σ₁	principal stress 1D - consider torsion due shear force is OFF: 1D - consider torsion due shear force is ON: 2D:	¹⁾ The angles of principal magnitudes are derived from to the local axis x. ²⁾The principal magnitudes can be visualized also as trajectories (see the option Trajectories in the command properties).
σ₂	principal stress
σ_E	equivalent stress (von Mises) 1D: 2D:
t_max,b(2D)	Maximum shear stress perpendicular to the plane

Membrane magnitudes (2D)

Value	Description	Notes
σ_mE	membrane equivalent stress (Mises)
σ_m1	principal membrane stress on positive face (max)
σ_m2	principal membrane stress on positive face (min)

Value

Description

Notes

σ_mE

membrane equivalent stress (Mises)

σ_m1

principal membrane stress on positive face (max)

σ_m2

principal membrane stress on positive face (min)

Basic total strain (2D)

The basic strains are default magnitudes referring to the local axes of the selected coordination system.

Value	Description	Notes
e_tot,x	strain on positive surface
e_tot,y	strain on positive surface
g_tot,xy	slope on positive surface

Value

Description

Notes

e_tot,x

strain on positive surface

e_tot,y

strain on positive surface

g_tot,xy

slope on positive surface

Principal total strain (2D)

The principal strains represent the extreme values of the internal forces derived from the basic ones by transformation into the directions of principal axes:

Value	Description	Notes
e_tot,1	maximum principal strain	principal strain on positive surface (max) principal strain on negative surface (max)
e_tot,2	maximum principal strain	principal strain on positive surface (min) principal strain on negative surface (min)
a	maximum angle of principal strain	angle of principal strain on positive surface angle of principal strain on negative surface
e_tot,M	maximum equivalent strain (Mises)	equivalent strain on positive surface (Mises) equivalent strain on negative surface (Mises)

Value

Description

Notes

e_tot,1

maximum principal strain

principal strain on positive surface (max)

principal strain on negative surface (max)

e_tot,2

maximum principal strain

principal strain on positive surface (min)

principal strain on negative surface (min)

maximum angle of principal strain

angle of principal strain on positive surface

angle of principal strain on negative surface

e_tot,M

maximum equivalent strain (Mises)

equivalent strain on positive surface (Mises)

equivalent strain on negative surface (Mises)

Basic plastic strain (2D)

The basic plastic strains are default magnitudes referring to the local axes of the selected coordination system. The basic plastic strains are part of basic total strains after nonlinear calculation with functionality "General plasticity" for elasto-plastic material.

Value	Description
e_pl,x	for elasto-plastic material without hardering for elasto-plastic material with hardering
e_pl,y
g_pl,xy

Value

Description

e_pl,x

for elasto-plastic material without hardering

for elasto-plastic material with hardering

e_pl,y

g_pl,xy

Principal plastic strain (2D)

The principal plastic strains represent the extreme values of the internal forces derived from the basic ones by transformation into the directions of principal axes. The principal plastic strains are part of principal total strains after nonlinear calculation with functionality "General plasticity" for elasto-plastic material.

Value	Description
e_pl,1	for elasto-plastic material without hardering for elasto-plastic material with hardering
e_pl,2
a
e_pl,M

Limitations

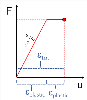
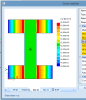
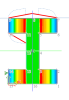
It is necessary to take into account that result are calculated in fibres only. Values between fibres are linearly interpolated. In some cases this precondition results in omitting of some local extremes. Example of this phenomenon is visible on following pictures:

There is a thick-walled I cross section exposed to horizontal shear force:

The third picture shows distribution of shear XY on the edge between fibres 7, 9. The theoretical distribution is shown by the dashed light blue line. the red line shows distribution which is presented by the 3D stress result. The reason is quite clear. The distribution of stresses is linear interpolation between values in fibres and the only fibre between fibres 7 and 9 is fibre 8 which has quite low value. Therefore the higher shear stress on exceeding parts of flanges are not respected on this edge.

This higher shear stress from exceeding part of flanges is displayed correctly on the inner edge 10-11 as is also visible on the picture.