Harmonic method - modal superposition
In the mode-superposition method, the factored mode shapes (obtained from a prior modal analysis) are summed to calculate the harmonic response of the analysed structure.
For this method of harmonic analysis, both types of damping are available: Rayleigh damping, as well as the Constant damping.
In case of modal superposition method, the additional dampers (finite elements) might not be used in the numerical model, as their damping constants (or damping properties) are not involved in the prior modal analysis (where only mass and stiffness matrix are involved). In case additional damping elements are desired to be used in the numerical model, Full Harmonic method needs to be used.
Results
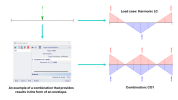
The Modal Superposition method provides positive and negative values of the response amplitude for each load case. In this way it also differs from Full Harmonic method, where only the absolute value of the response is available for load cases.
The user can determine the response of the structure to positive and negative amplitude of the excitation force by creating a combination. If the harmonic load case or the harmonic range load case is in a combination of the envelope type (see types of load case combinations), both positive and negative values of the response are automatically generated by applying the combination rules.